Is Pythagorean theorem really valid in higher dimensional space?
I saw that someone was writing Pythagorean theorem in 3 dimensional space. The equation was :
$$c=\sqrt{x^2+y^2+z^2}$$ If it's really correct than Pythagorean should work in higher dimensional space either. So I can write that
$$c=\sqrt{\sum_{n=0}^N x_n^2}$$
At first I was thinking how right triangle should look like in 3 dimensional space. From my imagination, the triangle will look like a pyramid but all sides of that pyramid will be looking like right triangle that's how Pythagorean works in 3 dimension. It's impossible to imagine the shape in 4 dimension or higher dimension.
Is Pythagorean theorem really valid in higher dimensional space?
2 answers
You are accessing this answer with a direct link, so it's being shown above all other answers regardless of its score. You can return to the normal view.
One generalization of the Pythagorean theorem to three dimensions is de Gua's theorem:
if a tetrahedron has a right-angle corner (like the corner of a cube), then the square of the area of the face opposite the right-angle corner is the sum of the squares of the areas of the other three faces
So the faces that are not opposite the right-angle corner act analogously to the non-hypotenuse sides of a right triangle, and the face that is opposite the right-angle corner is analogous to the hypotenuse. Instead of summing the squares of lengths of sides, you sum the squares of areas of faces.
This generalizes to higher dimensions: an $n$-dimensional simplex (a shape made of $n + 1$ vertices in $n$-dimensional space, all the edges that connect them, all the triangular faces that those edges create, all the tetrahedra that those triangles create, and so on up to $(n - 1)$-dimensional hyperfaces) with a vertex all of whose edges are pairwise perpendicular to each other will satisfy the property that the square of the measure (length, area, volume, etc.) of the hyperface that doesn't contain that vertex is equal to the sum of the squares of the measures of the other $n$ hyperfaces.
Another generalization of the Pythagorean theorem to three dimensions is simply the three-dimensional Euclidean metric: the square of the distance between two points in three-dimensional space is equal to the sum of the squares of the separation between those points along each of the coordinate axes, assuming some Cartesian coordinate system. In two dimensions, those axial separations form the sides of a right triangle, with the hypotenuse connecting the two points; but you could equivalently say that those axial separations form a rectangle, and the two points are connected by a diagonal of the rectangle. That latter visualization is more useful in higher dimensions: in three dimensions, you can't make a single triangle out of the segments anymore, but you can picture a rectangular prism formed by the two points on opposite corners with sides parallel to the coordinate axes, and the lengths being squared are three sides of the prism and its diagonal.
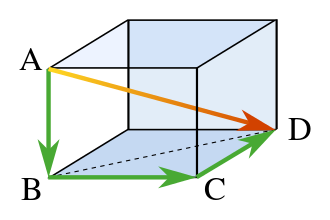
This too generalizes to $n$-prisms in $n$-dimensional space.
(And both of these generalizations are themselves special cases of this!)
0 comment threads
Consider a vector, $\mathbf v=(a,b,c)$, in $3$-space. We can project this onto the $xy$-plane, say, producing the vector $(a, b, 0)$ which we can identify with the $2$-vector, $(a, b)$. This two vector corresponds to the hypotenuse of a right triangle whose side lengths are $a$ and $b$. Therefore the squared length of this vector is $|(a,b)|^2 = a^2 + b^2$ according to the usual Pythagorean formula for a right triangle. But now we can consider the plane spanned by $(a,b,0)$ and $\mathbf v$, and in that plane view $v$ as the hypotenuse of a right triangle with side lengths $|(a,b)|$ and $c$. The squared length of the vector $\mathbf v$ is $|(a,b)|^2 + c^2 = a^2 + b^2 + c^2$. This logic can be extended to any dimension via an inductive argument showing that $|(a_1,\dots,a_n)|^2 = |(a_1,\dots a_{n-1})|^2 + a_n^2$.
That said, there are many other (probably better) ways of thinking about this. For example, any two vectors (in any dimension) gives rise to a (potentially degenerate) triangle in the plane spanned by those vectors (which will be ambiguous if they are linearly dependent). Namely, given vectors $\mathbf u$ and $\mathbf v$, we can consider the triangle $ABC$ such that the $A + \mathbf u = B$, $B + \mathbf v = C$ and thus $A + (\mathbf u + \mathbf v) = C$. The squared length of the "hypotenuse" $\overline{AC}$ is $$(\mathbf u + \mathbf v) \cdot (\mathbf u + \mathbf v) = \mathbf u \cdot \mathbf u + 2\mathbf u \cdot \mathbf v + \mathbf v \cdot \mathbf v$$ where $\cdot$ represents the dot or inner product and $\mathbf u^2 = |\mathbf u|^2 = \mathbf u \cdot \mathbf u$. The triangle will be a right triangle when $\mathbf u$ and $\mathbf v$ are orthogonal, i.e. at $\pm 90^\circ$ to each other in the plane they span. This is represented by $\mathbf u \cdot \mathbf v = 0 = |\mathbf u||\mathbf v|\cos(\pm 90^\circ)$. We now get a more abstract rendition of the Pythagorean theorem; now in any dimension and for any inner product space.




















0 comment threads