Post History
#3: Post edited
- One generalization of the Pythagorean theorem to three dimensions is [de Gua's theorem](https://en.wikipedia.org/wiki/De_Gua%27s_theorem):
- > if a tetrahedron has a right-angle corner (like the corner of a cube), then the square of the area of the face opposite the right-angle corner is the sum of the squares of the areas of the other three faces
- So the faces that are not opposite the right-angle corner act analogously to the non-hypotenuse sides of a right triangle, and the face that is opposite the right-angle corner is analogous to the hypotenuse. Instead of summing the squares of lengths of sides, you sum the squares of areas of faces.
- This generalizes to higher dimensions: an $n$-dimensional [simplex](https://en.wikipedia.org/wiki/Simplex) (a shape made of $n + 1$ vertices in $n$-dimensional space, all the edges that connect them, all the triangular faces that those edges create, all the tetrahedra that those triangles create, and so on up to $(n - 1)$-dimensional hyperfaces) with a vertex all of whose edges are pairwise perpendicular to each other will satisfy the property that the square of the measure (length, area, volume, etc.) of the hyperface that doesn't contain that vertex is equal to the sum of the squares of the measures of the other $n$ hyperfaces.
[Another generalization](https://en.wikipedia.org/wiki/Pythagorean_theorem#Solid_geometry) of the Pythagorean theorem to three dimensions is simply the three-dimensional Euclidean metric: the square of the distance between two points in three-dimensional space is equal to the sum of the squares of the separation between those points along each of the coordinate axes, assuming any orthogonal coordinate system. In two dimensions, those axial separations form the sides of a right triangle, with the hypotenuse connecting the two points; but you could equivalently say that those axial separations form a rectangle, and the two points are connected by a diagonal of the rectangle. That latter visualization is more useful in higher dimensions: in three dimensions, you can't make a single triangle out of the segments anymore, but you can picture a rectangular prism formed by the two points on opposite corners with sides parallel to the coordinate axes, and the lengths being squared are three sides of the prism and its diagonal.- 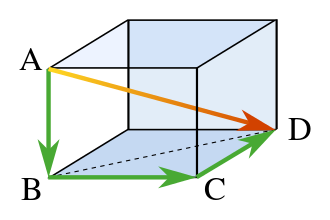
- This too generalizes to $n$-prisms in $n$-dimensional space.
- (And both of these generalizations are themselves special cases of [this](https://en.wikipedia.org/wiki/Pythagorean_theorem#Sets_of_m-dimensional_objects_in_n-dimensional_space)!)
- One generalization of the Pythagorean theorem to three dimensions is [de Gua's theorem](https://en.wikipedia.org/wiki/De_Gua%27s_theorem):
- > if a tetrahedron has a right-angle corner (like the corner of a cube), then the square of the area of the face opposite the right-angle corner is the sum of the squares of the areas of the other three faces
- So the faces that are not opposite the right-angle corner act analogously to the non-hypotenuse sides of a right triangle, and the face that is opposite the right-angle corner is analogous to the hypotenuse. Instead of summing the squares of lengths of sides, you sum the squares of areas of faces.
- This generalizes to higher dimensions: an $n$-dimensional [simplex](https://en.wikipedia.org/wiki/Simplex) (a shape made of $n + 1$ vertices in $n$-dimensional space, all the edges that connect them, all the triangular faces that those edges create, all the tetrahedra that those triangles create, and so on up to $(n - 1)$-dimensional hyperfaces) with a vertex all of whose edges are pairwise perpendicular to each other will satisfy the property that the square of the measure (length, area, volume, etc.) of the hyperface that doesn't contain that vertex is equal to the sum of the squares of the measures of the other $n$ hyperfaces.
- [Another generalization](https://en.wikipedia.org/wiki/Pythagorean_theorem#Solid_geometry) of the Pythagorean theorem to three dimensions is simply the three-dimensional Euclidean metric: the square of the distance between two points in three-dimensional space is equal to the sum of the squares of the separation between those points along each of the coordinate axes, assuming some Cartesian coordinate system. In two dimensions, those axial separations form the sides of a right triangle, with the hypotenuse connecting the two points; but you could equivalently say that those axial separations form a rectangle, and the two points are connected by a diagonal of the rectangle. That latter visualization is more useful in higher dimensions: in three dimensions, you can't make a single triangle out of the segments anymore, but you can picture a rectangular prism formed by the two points on opposite corners with sides parallel to the coordinate axes, and the lengths being squared are three sides of the prism and its diagonal.
- 
- This too generalizes to $n$-prisms in $n$-dimensional space.
- (And both of these generalizations are themselves special cases of [this](https://en.wikipedia.org/wiki/Pythagorean_theorem#Sets_of_m-dimensional_objects_in_n-dimensional_space)!)
#2: Post edited
One generalization of the Pythagorean theorem to three dimensions is [De Gua's theorem](https://en.wikipedia.org/wiki/De_Gua%27s_theorem):- > if a tetrahedron has a right-angle corner (like the corner of a cube), then the square of the area of the face opposite the right-angle corner is the sum of the squares of the areas of the other three faces
- So the faces that are not opposite the right-angle corner act analogously to the non-hypotenuse sides of a right triangle, and the face that is opposite the right-angle corner is analogous to the hypotenuse. Instead of summing the squares of lengths of sides, you sum the squares of areas of faces.
- This generalizes to higher dimensions: an $n$-dimensional [simplex](https://en.wikipedia.org/wiki/Simplex) (a shape made of $n + 1$ vertices in $n$-dimensional space, all the edges that connect them, all the triangular faces that those edges create, all the tetrahedra that those triangles create, and so on up to $(n - 1)$-dimensional hyperfaces) with a vertex all of whose edges are pairwise perpendicular to each other will satisfy the property that the square of the measure (length, area, volume, etc.) of the hyperface that doesn't contain that vertex is equal to the sum of the squares of the measures of the other $n$ hyperfaces.
- [Another generalization](https://en.wikipedia.org/wiki/Pythagorean_theorem#Solid_geometry) of the Pythagorean theorem to three dimensions is simply the three-dimensional Euclidean metric: the square of the distance between two points in three-dimensional space is equal to the sum of the squares of the separation between those points along each of the coordinate axes, assuming any orthogonal coordinate system. In two dimensions, those axial separations form the sides of a right triangle, with the hypotenuse connecting the two points; but you could equivalently say that those axial separations form a rectangle, and the two points are connected by a diagonal of the rectangle. That latter visualization is more useful in higher dimensions: in three dimensions, you can't make a single triangle out of the segments anymore, but you can picture a rectangular prism formed by the two points on opposite corners with sides parallel to the coordinate axes, and the lengths being squared are three sides of the prism and its diagonal.
- 
- This too generalizes to $n$-prisms in $n$-dimensional space.
- (And both of these generalizations are themselves special cases of [this](https://en.wikipedia.org/wiki/Pythagorean_theorem#Sets_of_m-dimensional_objects_in_n-dimensional_space)!)
- One generalization of the Pythagorean theorem to three dimensions is [de Gua's theorem](https://en.wikipedia.org/wiki/De_Gua%27s_theorem):
- > if a tetrahedron has a right-angle corner (like the corner of a cube), then the square of the area of the face opposite the right-angle corner is the sum of the squares of the areas of the other three faces
- So the faces that are not opposite the right-angle corner act analogously to the non-hypotenuse sides of a right triangle, and the face that is opposite the right-angle corner is analogous to the hypotenuse. Instead of summing the squares of lengths of sides, you sum the squares of areas of faces.
- This generalizes to higher dimensions: an $n$-dimensional [simplex](https://en.wikipedia.org/wiki/Simplex) (a shape made of $n + 1$ vertices in $n$-dimensional space, all the edges that connect them, all the triangular faces that those edges create, all the tetrahedra that those triangles create, and so on up to $(n - 1)$-dimensional hyperfaces) with a vertex all of whose edges are pairwise perpendicular to each other will satisfy the property that the square of the measure (length, area, volume, etc.) of the hyperface that doesn't contain that vertex is equal to the sum of the squares of the measures of the other $n$ hyperfaces.
- [Another generalization](https://en.wikipedia.org/wiki/Pythagorean_theorem#Solid_geometry) of the Pythagorean theorem to three dimensions is simply the three-dimensional Euclidean metric: the square of the distance between two points in three-dimensional space is equal to the sum of the squares of the separation between those points along each of the coordinate axes, assuming any orthogonal coordinate system. In two dimensions, those axial separations form the sides of a right triangle, with the hypotenuse connecting the two points; but you could equivalently say that those axial separations form a rectangle, and the two points are connected by a diagonal of the rectangle. That latter visualization is more useful in higher dimensions: in three dimensions, you can't make a single triangle out of the segments anymore, but you can picture a rectangular prism formed by the two points on opposite corners with sides parallel to the coordinate axes, and the lengths being squared are three sides of the prism and its diagonal.
- 
- This too generalizes to $n$-prisms in $n$-dimensional space.
- (And both of these generalizations are themselves special cases of [this](https://en.wikipedia.org/wiki/Pythagorean_theorem#Sets_of_m-dimensional_objects_in_n-dimensional_space)!)
#1: Initial revision
One generalization of the Pythagorean theorem to three dimensions is [De Gua's theorem](https://en.wikipedia.org/wiki/De_Gua%27s_theorem): > if a tetrahedron has a right-angle corner (like the corner of a cube), then the square of the area of the face opposite the right-angle corner is the sum of the squares of the areas of the other three faces So the faces that are not opposite the right-angle corner act analogously to the non-hypotenuse sides of a right triangle, and the face that is opposite the right-angle corner is analogous to the hypotenuse. Instead of summing the squares of lengths of sides, you sum the squares of areas of faces. This generalizes to higher dimensions: an $n$-dimensional [simplex](https://en.wikipedia.org/wiki/Simplex) (a shape made of $n + 1$ vertices in $n$-dimensional space, all the edges that connect them, all the triangular faces that those edges create, all the tetrahedra that those triangles create, and so on up to $(n - 1)$-dimensional hyperfaces) with a vertex all of whose edges are pairwise perpendicular to each other will satisfy the property that the square of the measure (length, area, volume, etc.) of the hyperface that doesn't contain that vertex is equal to the sum of the squares of the measures of the other $n$ hyperfaces. [Another generalization](https://en.wikipedia.org/wiki/Pythagorean_theorem#Solid_geometry) of the Pythagorean theorem to three dimensions is simply the three-dimensional Euclidean metric: the square of the distance between two points in three-dimensional space is equal to the sum of the squares of the separation between those points along each of the coordinate axes, assuming any orthogonal coordinate system. In two dimensions, those axial separations form the sides of a right triangle, with the hypotenuse connecting the two points; but you could equivalently say that those axial separations form a rectangle, and the two points are connected by a diagonal of the rectangle. That latter visualization is more useful in higher dimensions: in three dimensions, you can't make a single triangle out of the segments anymore, but you can picture a rectangular prism formed by the two points on opposite corners with sides parallel to the coordinate axes, and the lengths being squared are three sides of the prism and its diagonal.  This too generalizes to $n$-prisms in $n$-dimensional space. (And both of these generalizations are themselves special cases of [this](https://en.wikipedia.org/wiki/Pythagorean_theorem#Sets_of_m-dimensional_objects_in_n-dimensional_space)!)


















