How can I intuit $\dfrac{a - b}{c - d} \equiv \dfrac{{\color{red}{-}}(b - a)}{{\color{red}{-}}(d - c)} \equiv \dfrac{b - a}{d - c}$?
I'm not asking about algebra here which I can effortlessly effectuate. If helpful, let's intuit subtraction as facing backward, and the negative sign as backward steps. How does this intuition assist us to intuit $\dfrac{a - b}{c - d} \equiv \dfrac{{\color{red}{-}}(b - a)}{{\color{red}{-}}(d - c)} \equiv \dfrac{b - a}{d - c}$?
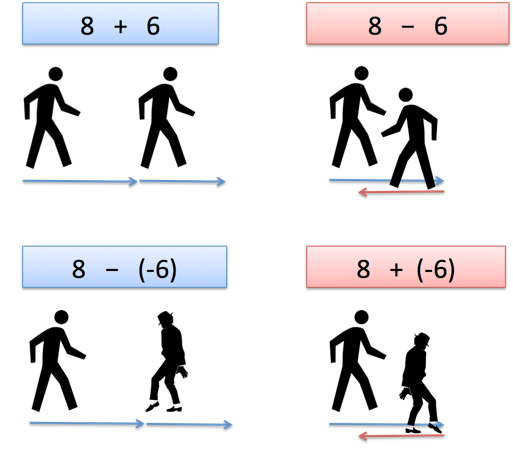
Ah! The addition/subtraction tells us which way to face, and the positive/negative tells us if our steps will be forward or backward (regardless of the way we're facing).
In a sense, the addition/subtraction acts as a verb ("face forward" or "face backward"), and the positive/negative acts as an adjective ("regular steps" or "backwards steps"). Or maybe it's an adverb, modifying how we walk (walk forwardly, walk backwardly). You get the idea.
1 answer
(1)
$$\dfrac{a - b}{c - d}$$
As the image depicts, $(a - b)$ means $a$ steps forward and $b$ steps backward which results in net $(a - b)$ steps, and dividing it by $(c - d)$ gives the number of steps (of length $(c - d)$) in $(a - b)$. Intuitive Meaning of Division can be found here.
(2) $$\dfrac{{{-}}(b - a)}{{{-}}(d - c)}$$
$-(b - a) \implies -[-(a-b)] \implies -(-a)+(-b)$ which means $a$ steps forward by facing backward and similarly $b$ steps backward which again results in net $(a - b)$ steps, dividing it by $-[-(c - d)]$ (here the negative sign indicates the way length $(c - d)$ was measured. See the figure) gives the number of steps (of length $(c - d)$) in $(a - b)$. Just like (1)
(3) $$\dfrac{b - a}{d - c}$$
Now can you intuite how is $\dfrac{b - a}{d - c}$ related to $\dfrac{a - b}{c - d}$ ?
P.S.: I have used 'length' in place of 'steps' in some sentences, this was done to not make the explanation complex. They don't really mean the same but are closely related.




















1 comment thread