Comments on How can I intuit $\dfrac{a - b}{c - d} \equiv \dfrac{{\color{red}{-}}(b - a)}{{\color{red}{-}}(d - c)} \equiv \dfrac{b - a}{d - c}$?
Post
How can I intuit $\dfrac{a - b}{c - d} \equiv \dfrac{{\color{red}{-}}(b - a)}{{\color{red}{-}}(d - c)} \equiv \dfrac{b - a}{d - c}$?
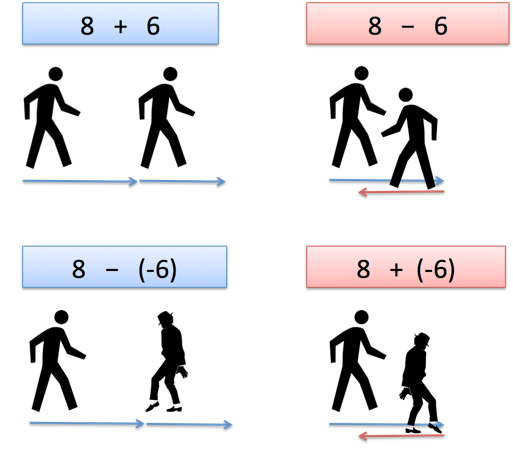
I'm not asking about algebra here which I can effortlessly effectuate. If helpful, let's intuit subtraction as facing backward, and the negative sign as backward steps. How does this intuition assist us to intuit $\dfrac{a - b}{c - d} \equiv \dfrac{{\color{red}{-}}(b - a)}{{\color{red}{-}}(d - c)} \equiv \dfrac{b - a}{d - c}$?
Ah! The addition/subtraction tells us which way to face, and the positive/negative tells us if our steps will be forward or backward (regardless of the way we're facing).
In a sense, the addition/subtraction acts as a verb ("face forward" or "face backward"), and the positive/negative acts as an adjective ("regular steps" or "backwards steps"). Or maybe it's an adverb, modifying how we walk (walk forwardly, walk backwardly). You get the idea.





















1 comment thread