Post History

60%

+1 −0

Q&A How can I intuit $\dfrac{a - b}{c - d} \equiv \dfrac{{\color{red}{-}}(b - a)}{{\color{red}{-}}(d - c)} \equiv \dfrac{b - a}{d - c}$?

posted 3y ago by Wolgwang‭ · edited 3y ago by Wolgwang‭

Answer

#2: Post edited by $user avatar$ Wolgwang‭ · 2021-08-14T18:38:58Z (over 3 years ago)
Added reference.

Copy Link

Raw

Markdown

**(1)**
$$\dfrac{a - b}{c - d}$$
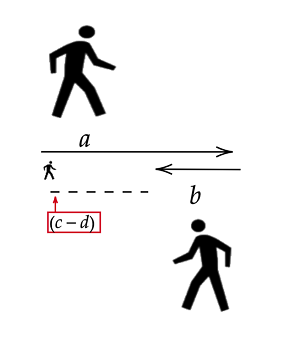
![Image 1](https://math.codidact.com/uploads/a8qAWGJyPTajXmh2RNpEnzrn)
As the image depicts, $(a - b)$ means $a$ steps forward and $b$ steps backward which results in net $(a - b)$ steps, and dividing it by $(c - d)$ gives the number of steps (of **length** $(c - d)$) in $(a - b)$.
<hr>
**(2)**
$$\dfrac{{{-}}(b - a)}{{{-}}(d - c)}$$
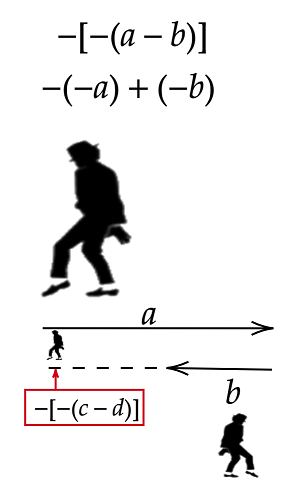
![Image 2](https://math.codidact.com/uploads/eUMqYu6B5SD2Z2K1N7g7aJv6)
$-(b - a) \implies -[-(a-b)] \implies -(-a)+(-b)$ which means $a$ steps forward by facing backward and similarly $b$ steps backward which again results in net $(a - b)$ steps, dividing it by $-[-(c - d)]$ (here the negative sign indicates the way length $(c - d)$ was measured. See the figure) gives the number of steps (of **length** $(c - d)$) in $(a - b)$.
Just like (1)
<hr>
**(3)**
$$\dfrac{b - a}{d - c}$$
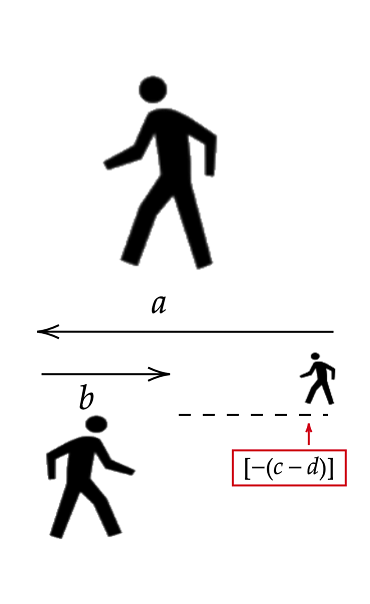
![Image 3](https://math.codidact.com/uploads/JmL7u3u9dJ3R77hMQ5LCfWCU)
Now can you intuite how is $\dfrac{b - a}{d - c}$ related to $\dfrac{a - b}{c - d}$ ?
<hr>
**P.S.:** I have used 'length' in place of 'steps' in some sentences, this was done to not make the explanation complex. They don't really mean the same but are closely related.

**(1)**
$$\dfrac{a - b}{c - d}$$
![Image 1](https://math.codidact.com/uploads/a8qAWGJyPTajXmh2RNpEnzrn)
As the image depicts, $(a - b)$ means $a$ steps forward and $b$ steps backward which results in net $(a - b)$ steps, and dividing it by $(c - d)$ gives the number of steps (of **length** $(c - d)$) in $(a - b)$.
Intuitive Meaning of Division can be found [here](https://betterexplained.com/articles/division-intuition/).
<hr>
**(2)**
$$\dfrac{{{-}}(b - a)}{{{-}}(d - c)}$$
![Image 2](https://math.codidact.com/uploads/eUMqYu6B5SD2Z2K1N7g7aJv6)
$-(b - a) \implies -[-(a-b)] \implies -(-a)+(-b)$ which means $a$ steps forward by facing backward and similarly $b$ steps backward which again results in net $(a - b)$ steps, dividing it by $-[-(c - d)]$ (here the negative sign indicates the way length $(c - d)$ was measured. See the figure) gives the number of steps (of **length** $(c - d)$) in $(a - b)$.
Just like (1)
<hr>
**(3)**
$$\dfrac{b - a}{d - c}$$
![Image 3](https://math.codidact.com/uploads/JmL7u3u9dJ3R77hMQ5LCfWCU)
Now can you intuite how is $\dfrac{b - a}{d - c}$ related to $\dfrac{a - b}{c - d}$ ?
<hr>
**P.S.:** I have used 'length' in place of 'steps' in some sentences, this was done to not make the explanation complex. They don't really mean the same but are closely related.

#1: Initial revision by $user avatar$ Wolgwang‭ · 2021-08-14T18:36:39Z (over 3 years ago)

Copy Link

Raw

Markdown

**(1)**

$$\dfrac{a - b}{c - d}$$

![Image 1](https://math.codidact.com/uploads/a8qAWGJyPTajXmh2RNpEnzrn)

As the image depicts, $(a - b)$ means $a$ steps forward and $b$ steps backward which results in net $(a - b)$ steps, and dividing it by $(c - d)$ gives the number of steps (of **length** $(c - d)$) in $(a - b)$.

<hr>


**(2)** 
$$\dfrac{{{-}}(b - a)}{{{-}}(d - c)}$$

![Image 2](https://math.codidact.com/uploads/eUMqYu6B5SD2Z2K1N7g7aJv6)

$-(b - a) \implies -[-(a-b)] \implies -(-a)+(-b)$ which means $a$ steps forward by facing backward and similarly $b$ steps backward which again results in net $(a - b)$ steps, dividing it by $-[-(c - d)]$ (here the negative sign indicates the way length $(c - d)$ was measured. See the figure) gives the number of steps (of **length** $(c - d)$) in $(a - b)$.
Just like (1)

<hr>

**(3)**
$$\dfrac{b - a}{d - c}$$


![Image 3](https://math.codidact.com/uploads/JmL7u3u9dJ3R77hMQ5LCfWCU)

Now can you intuite how is  $\dfrac{b - a}{d - c}$ related to $\dfrac{a - b}{c - d}$ ?

<hr>

**P.S.:** I have used 'length' in place of 'steps' in some sentences, this was done to not make the explanation complex. They don't really mean the same but are closely related.

Communities

Post History