Post History

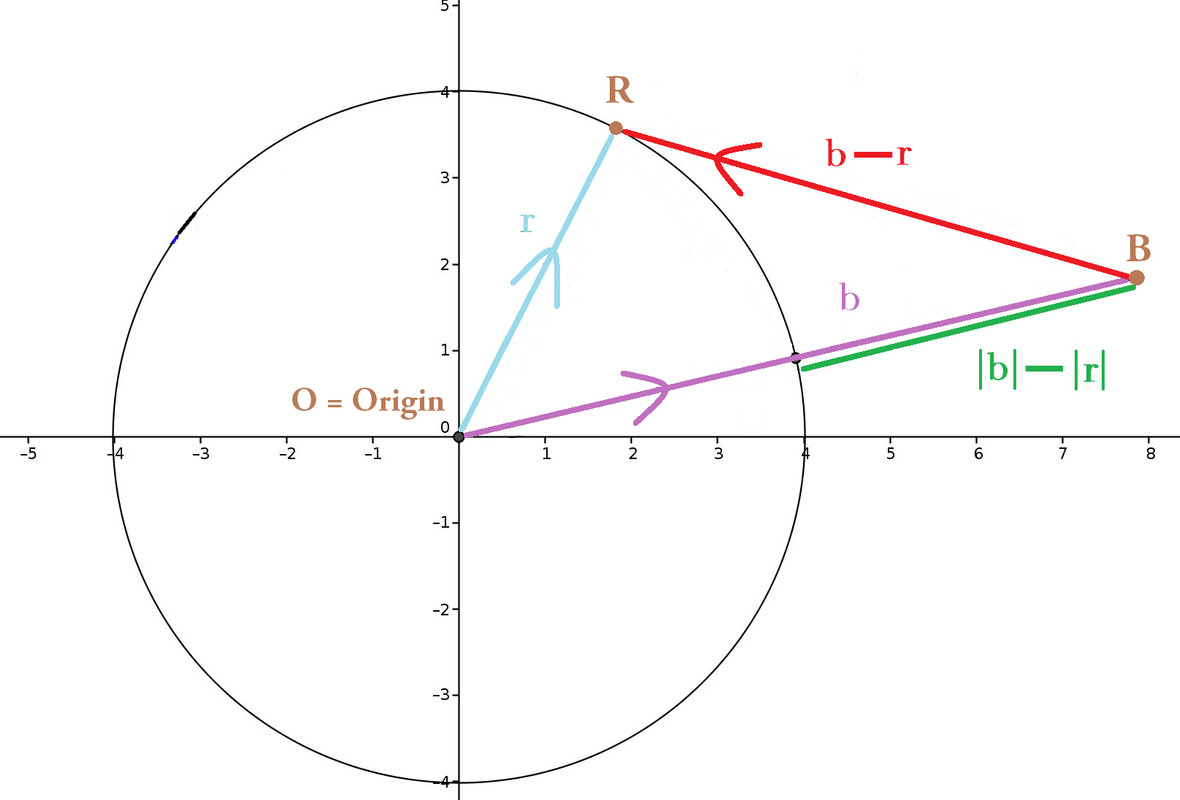
While pictorializing $|x - y|  < |x + y|$, how can 1 picture simultaneously prove (Reverse) △ Inequalities, $|x-y| ≤ |x|+|y|, |x|-|y| ≤ |x-y|$? 

I shall improve [this post](https://math.codidact.com/posts/289496), because 

- it overlooked Triangle Inequality, $|x + y| ≤ \color{darkgoldenrod}{|x| + |y|}$. Michael Spivak's *Calculus* (2008 4 edn) proved it on p. 12. 

- a distinctive diagram ought spotlight, and stress, that $|x - y|$ **_CAN_** $<  |x + y|.$

Ibid, exercise 12, p. 16.   

>(iv) ${\color{red}{|x-y|}} ≤ \color{goldenrod}{|x| + |y|}$. (Give a very short proof.)    
(v) ${\color{limegreen}{|x|-|y|}} ≤ {\color{red}{|x-y|}}$. (A very short proof is possible, if you write things in the right way).   

(vi)  $\left|{\color{limegreen}{|x|-|y|}}\right| ≤ |x  - y|$ (Why does this follow immediately from (v)?)    
**[This (vi) is the Reverse Triangle Inequality, but I deleted Spivak's superfluous set of round brackets.]**

#### In *SOLELY one and same* picture, please prove all 4 inequalities above? Remember to contrast $\vec{x}, \vec{y}$ so that visibly,  $|\vec{x} - \vec{y}| < |\vec{x} + \vec{y}|$.

Feel free to use my improvement of [this original](https://math.stackexchange.com/a/774233).

![](https://i.postimg.cc/Dys0bZwm/Reverse-Triangle-Inequality-Edited.jpg)