While pictorializing $|x - y| < |x + y|$, how can 1 picture simultaneously prove (Reverse) △ Inequalities, $|x-y| ≤ |x|+|y|, |x|-|y| ≤ |x-y|$? [duplicate]
Closed as duplicate by Peter Taylor on Sep 20, 2023 at 12:27
This question has been addressed elsewhere. See: 1 picture proof for the triangle inequality and the reverse triangle inequality
This question was closed; new answers can no longer be added. Users with the reopen privilege may vote to reopen this question if it has been improved or closed incorrectly.
I shall improve this post, because
-
it overlooked Triangle Inequality, $|x + y| ≤ \color{darkgoldenrod}{|x| + |y|}$. Michael Spivak's Calculus (2008 4 edn) proved it on p. 12.
-
a distinctive diagram ought spotlight, and stress, that $|x - y|$ CAN $< |x + y|.$
Ibid, exercise 12, p. 16.
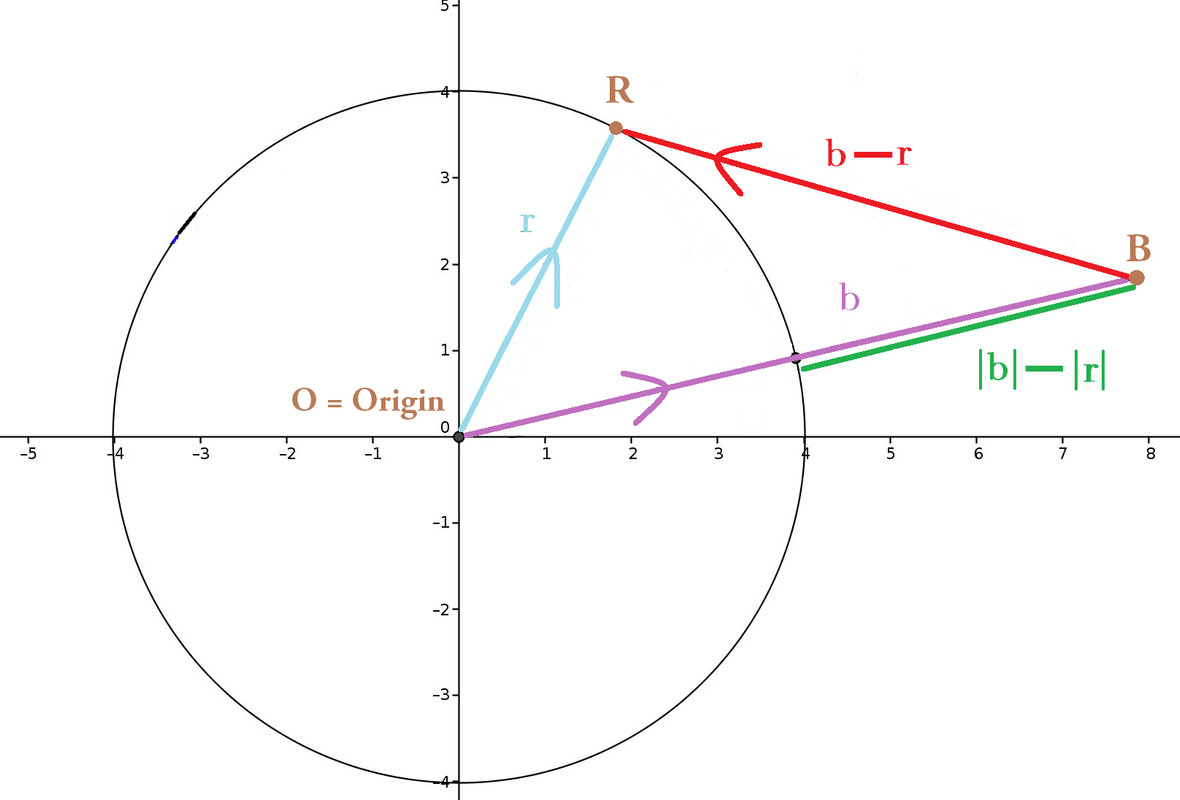
(iv) ${\color{red}{|x-y|}} ≤ \color{goldenrod}{|x| + |y|}$. (Give a very short proof.)
(v) ${\color{limegreen}{|x|-|y|}} ≤ {\color{red}{|x-y|}}$. (A very short proof is possible, if you write things in the right way).
(vi) $\left|{\color{limegreen}{|x|-|y|}}\right| ≤ |x - y|$ (Why does this follow immediately from (v)?)
[This (vi) is the Reverse Triangle Inequality, but I deleted Spivak's superfluous set of round brackets.]
In SOLELY one and same picture, please prove all 4 inequalities above? Remember to contrast $\vec{x}, \vec{y}$ so that visibly, $|\vec{x} - \vec{y}| < |\vec{x} + \vec{y}|$.
Feel free to use my improvement of this original.




















2 comment threads