Post History
#2: Post edited
- I call graphs $G_1$ and $G_2$ _distinct_ iff (i) $G_1$ has a different arrangement<sup>1</sup> of vertices than $G_2$ **and** (ii) $G_1$ and $G_2$ have the same number of vertices. All other properties of $G_1$ and $G_2$ have no effect on distinguishing them. For example, $G_1$ and $G_2$ may be the _same_ even if the number of edges of the two graphs is different.
- ----
- **Example:**
- | $G_1$ | $G_2$ | $G_3$ |
- | - | - | - |
- | 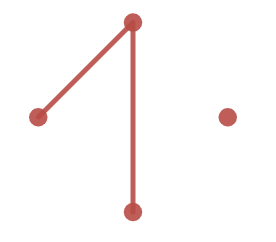| | |
- Here, $G_1 = G_2$ but $G_1 \neq G_3 \iff G_2 \neq G_3$.
- ----
- I'm wondering if there is a way to create a unique correspondence between a graph and a single _word_ (any string of letters, possibly gibberish) of the English alphabet. That is to say, _distinct_ graphs $G_1$ and $G_2$ must necessarily map to a different _word_. It is preferable that the _word_ has 4-7 characters. Additionally, the _word_ **may** contain a single integer from 1-9 at the end of it. Hence, for example, $G_1$ could map to the _word_ GLBXR7 and $G_2$ could map to the word MMTR.
- > I'm looking for an _algorithm_ to map every _distinct_ graph with a unique _word_. You may assume that every graph has the same number of vertices.
- A very crude attempt is to label each vertex of a graph with letters from left to right, top to bottom and concatenate them in that order. However, I don’t think this is sufficient for uniqueness.
- -----
- <sup>1</sup><sub>I'm not sure how to perfectly formalise the notion of an arrangement, but a possible necessary and sufficient condition is to consider the number of vertices to the left, right and along the same vertical axis as each vertex of graphs $G_1$ and $G_2$—if any of the values are different, the graphs are _distinct_.</sub>
- I call graphs $G_1$ and $G_2$ _distinct_ iff (i) $G_1$ has a different arrangement<sup>1</sup> of vertices than $G_2$ **and** (ii) $G_1$ and $G_2$ have the same number of vertices. All other properties of $G_1$ and $G_2$ have no effect on distinguishing them. For example, $G_1$ and $G_2$ may be the _same_ even if the number of edges of the two graphs is different.
- ----
- **Example:**
- | $G_1$ | $G_2$ | $G_3$ |
- | - | - | - |
- | | | |
- Here, $G_1 = G_2$ but $G_1 \neq G_3 \iff G_2 \neq G_3$.
- ----
- I'm wondering if there is a way to create a unique correspondence between a graph and a single _word_ (any string of letters, possibly gibberish) of the English alphabet. That is to say, _distinct_ graphs $G_1$ and $G_2$ must necessarily map to a different _word_. It is preferable that the _word_ has 4-7 characters. Additionally, the _word_ **may** contain a single integer from 1-9 at the end of it. Hence, for example, $G_1$ could map to the _word_ GLBXR7 and $G_2$ could map to the word MMTR.
- > I'm looking for an _algorithm_ to map every _distinct_ graph with a unique _word_. You may assume that every graph has the same number of vertices.
- A very crude attempt is to label each vertex of a graph with letters from left to right, top to bottom and concatenate them in that order. However, I don’t think this is sufficient for uniqueness.
- Clarifications
- -
- I attempt to clarify some of the potentially ambiguous elements of my post.
- 1. I agree that the notion of a "graph" is not entirely relevant here. I actually chose it because I am working with this sort of information in another project where connectivity matters. Nonetheless, viewing this as a point cloud is perfectly fine; you may edit the tag(s) if you'd like.
- 2. There doesn’t need to be a bijection between words and graphs. Every unique graph should map to a unique word, but every word need not map to a graph.
- 3. Since I placed a finite restriction on the length of a word (4 - 7 characters), I attempt to set an upper bound on the number of vertices of a graph.
- $$\text{Number of words} = \sum_{k = 4}^7 \left(26^{k-1}\cdot (26 + 9)\right) = 11244509640$$
- $$\text{Number of graphs with} \le n \\; \text{vertices} = \sum_{k = 1}^n \sum_{i = 1}^k {{k - 1} \choose {i - 1}} = 2^n - 1$$
- $$11244509640 = 2^n - 1 \implies \lfloor n\rfloor = 33$$
- 4. I apologise for not making this point before, but the _algorithm_ should be human computable, that is, possibly something a human can do in their head in about 15 seconds.
- -----
- <sup>1</sup><sub>I'm not sure how to perfectly formalise the notion of an arrangement, but a possible necessary and sufficient condition is to consider the number of vertices to the left, right and along the same vertical axis as each vertex of graphs $G_1$ and $G_2$—if any of the values are different, the graphs are _distinct_.</sub>
#1: Initial revision
Is there a way to encode a unique arrangement of vertices of a graph with a unique short word?
I call graphs $G_1$ and $G_2$ _distinct_ iff (i) $G_1$ has a different arrangement<sup>1</sup> of vertices than $G_2$ **and** (ii) $G_1$ and $G_2$ have the same number of vertices. All other properties of $G_1$ and $G_2$ have no effect on distinguishing them. For example, $G_1$ and $G_2$ may be the _same_ even if the number of edges of the two graphs is different. ---- **Example:** | $G_1$ | $G_2$ | $G_3$ | | - | - | - | | | | | Here, $G_1 = G_2$ but $G_1 \neq G_3 \iff G_2 \neq G_3$. ---- I'm wondering if there is a way to create a unique correspondence between a graph and a single _word_ (any string of letters, possibly gibberish) of the English alphabet. That is to say, _distinct_ graphs $G_1$ and $G_2$ must necessarily map to a different _word_. It is preferable that the _word_ has 4-7 characters. Additionally, the _word_ **may** contain a single integer from 1-9 at the end of it. Hence, for example, $G_1$ could map to the _word_ GLBXR7 and $G_2$ could map to the word MMTR. > I'm looking for an _algorithm_ to map every _distinct_ graph with a unique _word_. You may assume that every graph has the same number of vertices. A very crude attempt is to label each vertex of a graph with letters from left to right, top to bottom and concatenate them in that order. However, I don’t think this is sufficient for uniqueness. ----- <sup>1</sup><sub>I'm not sure how to perfectly formalise the notion of an arrangement, but a possible necessary and sufficient condition is to consider the number of vertices to the left, right and along the same vertical axis as each vertex of graphs $G_1$ and $G_2$—if any of the values are different, the graphs are _distinct_.</sub>


















