Post History

How does counting E twice explain the discrepancy between the third between C and E, third between E and G, but fifth between C and G?

I still don't grasp the "source of the discrepancy". "the E got counted twice when we went C,D,E and then E,F,G, but only got counted once when we went C,D,E,F,G." — So what? How does this expound the discrepancy? 

[Impaled on a Fencepost |](https://mathenchant.wordpress.com/2017/11/16/impaled-on-a-fencepost/)

> The music theorists of the Middle Ages committed a fencepost error that’s too entrenched to dig up now. Consider the chord made of the notes C, E, and G (a C major triad). If music theory nomenclature for intervals made sense, the distance from C up to E plus the distance from E up to G would equal the distance from C up to G. And that’s true if you measure the intervals by counting upward steps. The problem comes when you describe intervals with what I suppose might be termed “ordinal nomenclature”: going from C to E is called going up by a third (because you count 1,2,3 when you play C,D,E) and going from E to G is called going up by a third for the same reason, but going from C to G is called going up by a fifth (because you count 1,2,3,4,5 as you play C,D,E,F,G).
> 
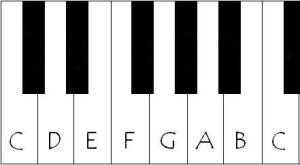> [![](https://mathenchant.files.wordpress.com/2017/11/029-piano.jpg?w=300&h=166)](https://mathenchant.files.wordpress.com/2017/11/029-piano.jpg)The source of the discrepancy should be clear: the E got counted twice when we went C,D,E and then E,F,G, but only got counted once when we went C,D,E,F,G. So in music theory, when you stack a third on top of a third, you get a fifth. We musicians are stuck with nomenclature that essentially makes us say “3+3=5” so many times that we eventually stop noticing we’re saying it. (Of course, saying “a third plus a third is a fifth” is confusing on a different level, since it sounds like “1/3 + 1/3 = 1/5”. But I digress.)