Comments on How can Cross Multiplication be intuited or pictured?
Post
How can Cross Multiplication be intuited or pictured? [closed]
+0
−3
Closed as unclear by Peter Taylor on Nov 27, 2021 at 20:58
This question cannot be answered in its current form, because critical information is missing.
This question was closed; new answers can no longer be added. Users with the reopen privilege may vote to reopen this question if it has been improved or closed incorrectly.
I already know, I'm NOT asking about, the algebra. It's NOT intuitive why 3 pears x 4 tangelos = 6 quinces x 2 riberries $\iff$ 3 pears/6 quinces = 2 riberries/4 tangelos.
I stumbled the picture below, but how does it proffer intuition?



















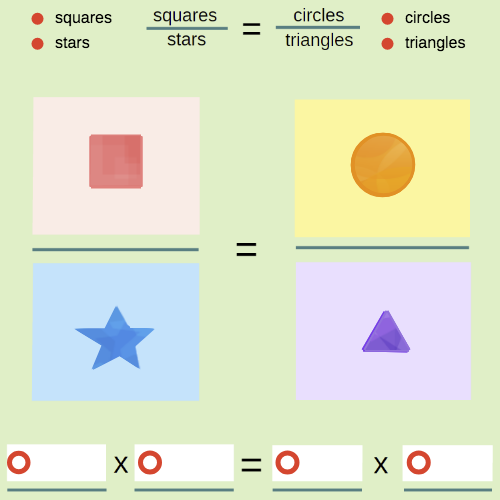

2 comment threads