Post History

Yes, most of the simpler fractals are like this. For instance, in the Sierpinski gasket, each of the three corner triangles is made up of a copy of the whole.

![The Sierpinski gasket](https://math.codidact.com/uploads/985vktnxmeosbbqdue8j43mlciz2)

In fact, this is a _defining property_ of the gasket: that is, if we state that there is a figure with the property such that it consists of three copies of the whole, shrunk by 50%, and arranged with two copies next to each other, and one on top in the middle, then we must be talking about the Sierpinski triangle.

Here is another example: the Koch curve.

![The Koch curve.](https://math.codidact.com/uploads/vqr72ngtzbzp04uxgqhh3wrj18m8)

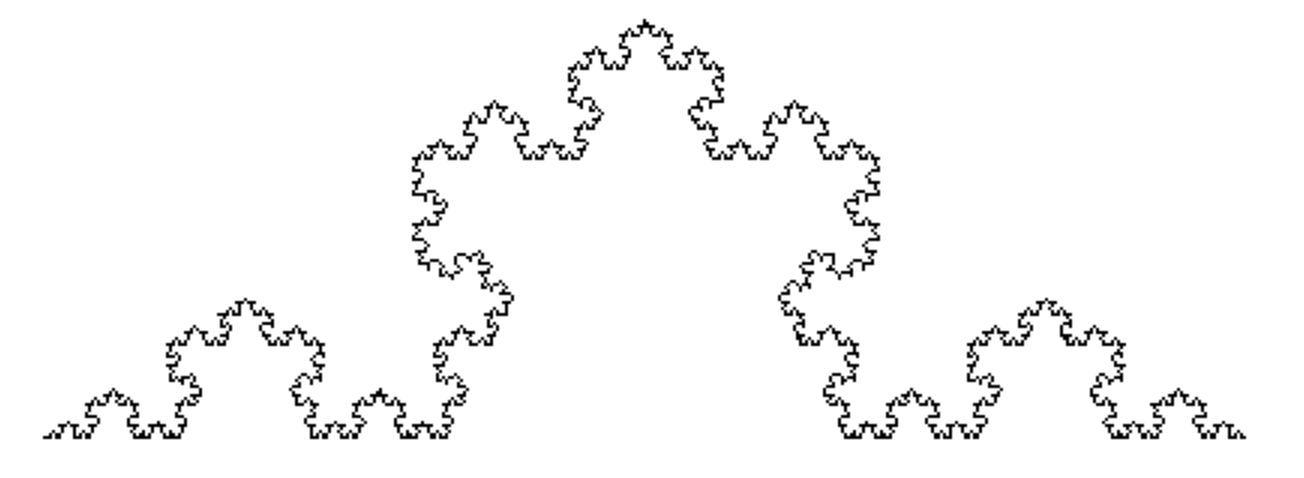
The Koch curve has the interesting property that there are two ways of defining it in terms of copies of the whole. You can shrink two copies by about half and place them upside-down, next to each other at a slight angle, or you can take four copies and arrange them with two flat ones on either side and two in the middle angled up. 

These are called [Iterated Function Systems](https://en.wikipedia.org/wiki/Iterated_function_system) (IFSs). Any set of two or more maps that are contractive on average will produce a IFS with the property you describe: if you zoom in on the right spot, you see a smaller copy of the whole.

The relation to number systems that you mention also exists. For instance, we can encode each "subtriangle" on the Sierpinski gasket by which of the three transformations (0,1 or 2) we need to apply to get to that triangle. Applying this recursively, can encode smaller and smaller regions of space by longer sequences of these three digits.

![Codes on the Sierpinski gasket.](https://math.codidact.com/uploads/2ff1nf6ldck653mvrf8pkq7y5459)

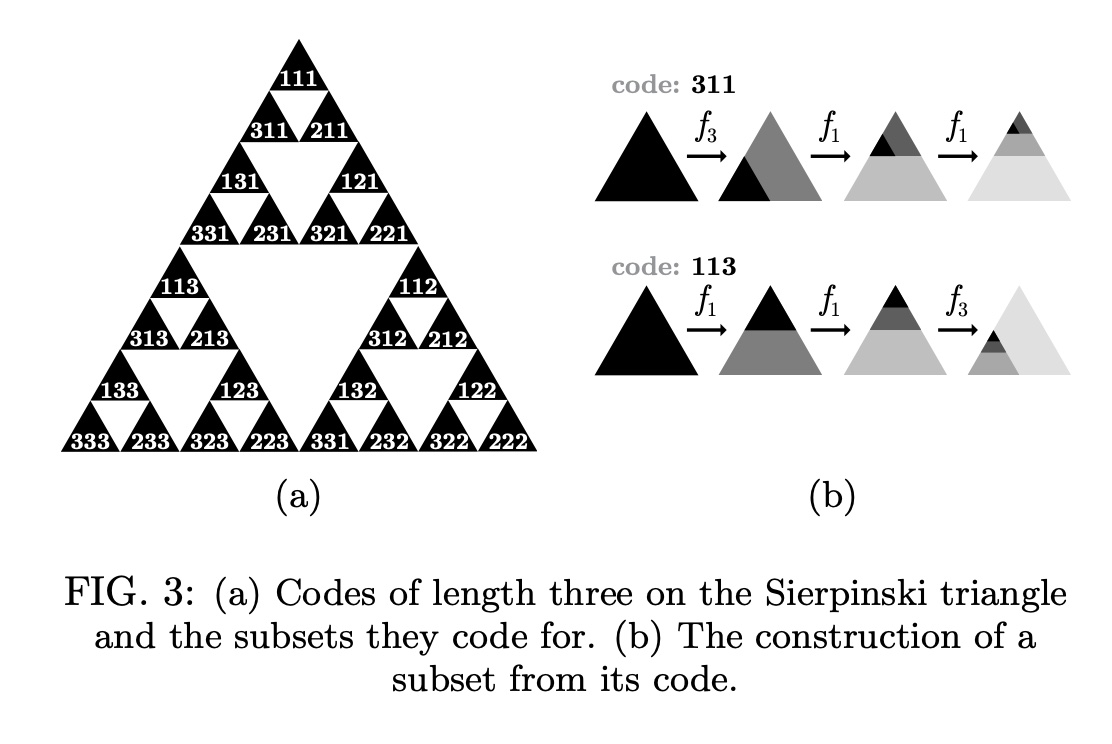
_From [this paper](https://arxiv.org/abs/1706.03149v2) by yours truly._

You can see the relation to real numbers if you imagine the interval [0,1) as an IFS with two copies: the top and bottom half are both copies of the whole. Then, the corresponding codes give you a binary sequence for each diadic interval, which in the limit form the binary decimal expansions of a real number. 

Interestingly, the Mandelbrot set has this property approximately. If you zoom in on the right places, you will see many "mini-mandelbrots", sometimes called "satellites".

![A mandelbrot satellite.](https://math.codidact.com/uploads/j1chk78hba0zg3p3xk5owy1pmylz) 

_Created by Wolfgang Beyer with the program Ultra Fractal 3. - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=322028_

The larger structure of the Mandelbrot also allows for other "looping zooms", as shown in [this gif](https://en.wikipedia.org/wiki/Mandelbrot_set#/media/File:Self-Similarity-Zoom.gif).