Post History
#9: Post edited
- Yes, your right the axioms are (usually) written in first-order logic (FOL).
- However, we can "cheat" by using natural language to describe our axioms (which is done in the Wikipedia article).
- After all at some point some axioms will need to be defined in natural language.
- (e.g.: If Peano Axioms are defined in FOL, then what is FOL defined with?)
- Therefore to make them "primitive notions", we simply cheat by defining them in natural language.
- ### Why do we need these axioms specifically?
- The Peano Axioms (PA) are:
- * a) 0 is a natural number
- * b) For all natural numbers $n$, $S(n)$ is a natural number
- * c) For all natural numbers $n$ & $m$, if $S(n) = S(m)$, then $n = m$
- * d) For all natural numbers $n$, $S(n) = 0$ is false
- * e) Given a set $K$ which contains $0$,
- If whenever a natural numbers $n$ is in $K$ also means $S(n)$ is in $K$,
- Then $K$ contains all natural numbers.
- So the first 2 axioms are pretty intuitive, as they're required to create a structure with multiple elements:
- * a) We have the natural number: $0$
- *"We need a starting point"*
- * b) We now have natural numbers: $0, S(0), S(S(0)), ...$
- *"We can take steps from the starting point"*
- Now at this point, the natural numbers *could* be several sets. The following are alternative systems that have yet to be disqualified, meaning the first two axioms don't describe $\mathbb{N}$ in a satisfactory way:
- 1. **Preorder-like structure:**
- $\{ 0, a, S(0) \}$ where $S(0) = S(a)$ and $S(S(0)) = 0$
- 2. **Cyclic structure:**
- $\{ 0, S(0), S(S(0)) \}$ and $S(S(S(0))) = 0$ or $\{ 0, 1, 2 \}$ are the only numbers and $2 + 1 = 0$
- 3. **Two zeros:**
- $\{ 0, a, S(0), S(a), S(S(0)), \dots \}$ where $a \neq 0$
- Graphically, we can visualize these in the following way:
- 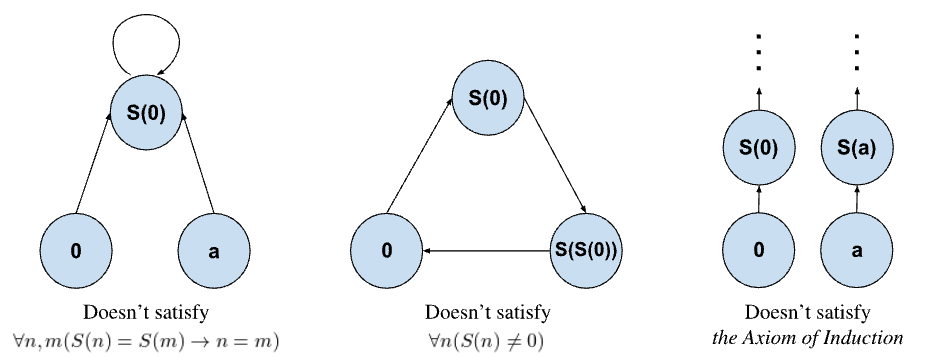
- These structures are successfully ruled out by the remaining axioms:
- * Axiom (c) successfully rules out (1) since $S(0) = S(a)$, but $a \neq 0$.
- We can interpret (c) as a type of linearization axiom where:
- *"There is only one path to get to a number by successive steps"*
- * Axiom (d) successfully rules out (2) since $S(S(0)) = 0$ contradicting the axiom.
- We can interpret (d) as a no-loops axiom where:
- *"There is no number whose next number is zero"*
- **(Notice this also rules out negative numbers, so it's also a no-negatives axiom)**
- * Axiom (e) intuitively means: all natural numbers can be obtained by applying $S$ to $0$.
- This fails for (3), since $a$ cannot be obtained by applying $S$ to $0$. One way to put it is:
- *"All natural numbers are obtained from 0"*
- Now, one might think: *are these axioms sufficient? Do we know if these actually are the natural numbers we think of intuitively?* The answer to both is *"we don't know"*. They seem to be sufficient for proving standard results in number theory, however whether they are *"actually the natural numbers"* is a philosophical question.
- Of course there also different axioms which can define this same structure. But these ones just happened to become standard for historical & practical reasons.
- ### Regarding the axioms of equality
- Notice that we used the notion of equality several times when defining the axioms. We used an operator $=$, and we forgot to define it.
- While we could argue that "equality is intuitive", formally it should be specified. This is what the equality axioms do.
- ### Regarding the axiom of induction
- The reason why this is a second-order statement, is actually hidden in our formulation. Notice however that we used the notion of a "set" in the definition. This is where the "second-order"-ness is coming in.
- We are saying something about "all sets", meaning we are using a quantifier over the "sets". This is what is second-order about it.
- Another formulation of the axioms where $P$ is a predicate is:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- You can change $P(x)$ to $x \in K$ to get the same definition we used earlier. Notice that $\forall P$ is a quantifier over all predicates, whereas $\forall n$ is a quantifier over all numbers.
- Having $\forall P$ is what makes it a second-order statement.
- So yes, this can be understood as having bound variables which are first-order sentences themselves.
- ### Relation to second-order arithmetic
- The axiom of induction makes the formulation close to second-order arithmetic since second-order arithmetic uses:
- * The axiom of induction
- * The axiom of comprehension
- Thus we only need one more axiom to reach it. I won't go into much more detail, but in essence second-order arithmetic lets us define reals & rationals making is significantly stronger than PA.
- ### Peano Axioms as a first-order theory
- The axioms I presented earlier include a second-order axiom (the axiom of induction), as I discussed earlier. We can weaken it into a first-order theory by using an axiom schema.
- An axiom schema is simply an infinite list of axioms. So in this case, we can have a weaker version of:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- Where instead we say:
- 1. Generate a first-order formula $P$ (which we haven't generated yet)
- 2. Add the rule:
- $$P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n))$$
- This in essence makes the list of possible $P$ countable (whereas it was uncountable before).
It turns out this limits the types of sets in PA significantly.Therefore the PA we defined earlier is stronger than this theory, but weaker than second-order arithmetic.
- Yes, your right the axioms are (usually) written in first-order logic (FOL).
- However, we can "cheat" by using natural language to describe our axioms (which is done in the Wikipedia article).
- After all at some point some axioms will need to be defined in natural language.
- (e.g.: If Peano Axioms are defined in FOL, then what is FOL defined with?)
- Therefore to make them "primitive notions", we simply cheat by defining them in natural language.
- ### Why do we need these axioms specifically?
- The Peano Axioms (PA) are:
- * a) 0 is a natural number
- * b) For all natural numbers $n$, $S(n)$ is a natural number
- * c) For all natural numbers $n$ & $m$, if $S(n) = S(m)$, then $n = m$
- * d) For all natural numbers $n$, $S(n) = 0$ is false
- * e) Given a set $K$ which contains $0$,
- If whenever a natural numbers $n$ is in $K$ also means $S(n)$ is in $K$,
- Then $K$ contains all natural numbers.
- So the first 2 axioms are pretty intuitive, as they're required to create a structure with multiple elements:
- * a) We have the natural number: $0$
- *"We need a starting point"*
- * b) We now have natural numbers: $0, S(0), S(S(0)), ...$
- *"We can take steps from the starting point"*
- Now at this point, the natural numbers *could* be several sets. The following are alternative systems that have yet to be disqualified, meaning the first two axioms don't describe $\mathbb{N}$ in a satisfactory way:
- 1. **Preorder-like structure:**
- $\{ 0, a, S(0) \}$ where $S(0) = S(a)$ and $S(S(0)) = 0$
- 2. **Cyclic structure:**
- $\{ 0, S(0), S(S(0)) \}$ and $S(S(S(0))) = 0$ or $\{ 0, 1, 2 \}$ are the only numbers and $2 + 1 = 0$
- 3. **Two zeros:**
- $\{ 0, a, S(0), S(a), S(S(0)), \dots \}$ where $a \neq 0$
- Graphically, we can visualize these in the following way:
- 
- These structures are successfully ruled out by the remaining axioms:
- * Axiom (c) successfully rules out (1) since $S(0) = S(a)$, but $a \neq 0$.
- We can interpret (c) as a type of linearization axiom where:
- *"There is only one path to get to a number by successive steps"*
- * Axiom (d) successfully rules out (2) since $S(S(0)) = 0$ contradicting the axiom.
- We can interpret (d) as a no-loops axiom where:
- *"There is no number whose next number is zero"*
- **(Notice this also rules out negative numbers, so it's also a no-negatives axiom)**
- * Axiom (e) intuitively means: all natural numbers can be obtained by applying $S$ to $0$.
- This fails for (3), since $a$ cannot be obtained by applying $S$ to $0$. One way to put it is:
- *"All natural numbers are obtained from 0"*
- Now, one might think: *are these axioms sufficient? Do we know if these actually are the natural numbers we think of intuitively?* The answer to both is *"we don't know"*. They seem to be sufficient for proving standard results in number theory, however whether they are *"actually the natural numbers"* is a philosophical question.
- Of course there also different axioms which can define this same structure. But these ones just happened to become standard for historical & practical reasons.
- ### Regarding the axioms of equality
- Notice that we used the notion of equality several times when defining the axioms. We used an operator $=$, and we forgot to define it.
- While we could argue that "equality is intuitive", formally it should be specified. This is what the equality axioms do.
- ### Regarding the axiom of induction
- The reason why this is a second-order statement, is actually hidden in our formulation. Notice however that we used the notion of a "set" in the definition. This is where the "second-order"-ness is coming in.
- We are saying something about "all sets", meaning we are using a quantifier over the "sets". This is what is second-order about it.
- Another formulation of the axioms where $P$ is a predicate is:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- You can change $P(x)$ to $x \in K$ to get the same definition we used earlier. Notice that $\forall P$ is a quantifier over all predicates, whereas $\forall n$ is a quantifier over all numbers.
- Having $\forall P$ is what makes it a second-order statement.
- So yes, this can be understood as having bound variables which are first-order sentences themselves.
- ### Relation to second-order arithmetic
- The axiom of induction makes the formulation close to second-order arithmetic since second-order arithmetic uses:
- * The axiom of induction
- * The axiom of comprehension
- Thus we only need one more axiom to reach it. I won't go into much more detail, but in essence second-order arithmetic lets us define reals & rationals making is significantly stronger than PA.
- ### Peano Axioms as a first-order theory
- The axioms I presented earlier include a second-order axiom (the axiom of induction), as I discussed earlier. We can weaken it into a first-order theory by using an axiom schema.
- An axiom schema is simply an infinite list of axioms. So in this case, we can have a weaker version of:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- Where instead we say:
- 1. Generate a first-order formula $P$ (which we haven't generated yet)
- 2. Add the rule:
- $$P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n))$$
- 3. Repeat step 1.
- This in essence makes the list of possible $P$ countable (whereas it was uncountable before).
- It turns out this limits PA significantly (e.g.: many sets and multiplication cannot be easily defined). Therefore the PA we defined earlier is stronger than this theory, but weaker than second-order arithmetic.
#8: Post edited
- Yes, your right the axioms are (usually) written in first-order logic (FOL).
- However, we can "cheat" by using natural language to describe our axioms (which is done in the Wikipedia article).
- After all at some point some axioms will need to be defined in natural language.
- (e.g.: If Peano Axioms are defined in FOL, then what is FOL defined with?)
- Therefore to make them "primitive notions", we simply cheat by defining them in natural language.
- ### Why do we need these axioms specifically?
- The Peano Axioms (PA) are:
- * a) 0 is a natural number
- * b) For all natural numbers $n$, $S(n)$ is a natural number
- * c) For all natural numbers $n$ & $m$, if $S(n) = S(m)$, then $n = m$
- * d) For all natural numbers $n$, $S(n) = 0$ is false
- * e) Given a set $K$ which contains $0$,
- If whenever a natural numbers $n$ is in $K$ also means $S(n)$ is in $K$,
- Then $K$ contains all natural numbers.
So the first 2 axioms are pretty intuitive, as they're required to create any structure with multiple elements:- * a) We have the natural number: $0$
- *"We need a starting point"*
- * b) We now have natural numbers: $0, S(0), S(S(0)), ...$
- *"We can take steps from the starting point"*
- Now at this point, the natural numbers *could* be several sets. The following are alternative systems that have yet to be disqualified, meaning the first two axioms don't describe $\mathbb{N}$ in a satisfactory way:
- 1. **Preorder-like structure:**
- $\{ 0, a, S(0) \}$ where $S(0) = S(a)$ and $S(S(0)) = 0$
- 2. **Cyclic structure:**
- $\{ 0, S(0), S(S(0)) \}$ and $S(S(S(0))) = 0$ or $\{ 0, 1, 2 \}$ are the only numbers and $2 + 1 = 0$
- 3. **Two zeros:**
- $\{ 0, a, S(0), S(a), S(S(0)), \dots \}$ where $a \neq 0$
- Graphically, we can visualize these in the following way:
- 
- These structures are successfully ruled out by the remaining axioms:
- * Axiom (c) successfully rules out (1) since $S(0) = S(a)$, but $a \neq 0$.
- We can interpret (c) as a type of linearization axiom where:
- *"There is only one path to get to a number by successive steps"*
- * Axiom (d) successfully rules out (2) since $S(S(0)) = 0$ contradicting the axiom.
- We can interpret (d) as a no-loops axiom where:
- *"There is no number whose next number is zero"*
- **(Notice this also rules out negative numbers, so it's also a no-negatives axiom)**
- * Axiom (e) intuitively means: all natural numbers can be obtained by applying $S$ to $0$.
- This fails for (3), since $a$ cannot be obtained by applying $S$ to $0$. One way to put it is:
- *"All natural numbers are obtained from 0"*
- Now, one might think: *are these axioms sufficient? Do we know if these actually are the natural numbers we think of intuitively?* The answer to both is *"we don't know"*. They seem to be sufficient for proving standard results in number theory, however whether they are *"actually the natural numbers"* is a philosophical question.
- Of course there also different axioms which can define this same structure. But these ones just happened to become standard for historical & practical reasons.
- ### Regarding the axioms of equality
- Notice that we used the notion of equality several times when defining the axioms. We used an operator $=$, and we forgot to define it.
- While we could argue that "equality is intuitive", formally it should be specified. This is what the equality axioms do.
- ### Regarding the axiom of induction
- The reason why this is a second-order statement, is actually hidden in our formulation. Notice however that we used the notion of a "set" in the definition. This is where the "second-order"-ness is coming in.
- We are saying something about "all sets", meaning we are using a quantifier over the "sets". This is what is second-order about it.
- Another formulation of the axioms where $P$ is a predicate is:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- You can change $P(x)$ to $x \in K$ to get the same definition we used earlier. Notice that $\forall P$ is a quantifier over all predicates, whereas $\forall n$ is a quantifier over all numbers.
- Having $\forall P$ is what makes it a second-order statement.
- So yes, this can be understood as having bound variables which are first-order sentences themselves.
- ### Relation to second-order arithmetic
- The axiom of induction makes the formulation close to second-order arithmetic since second-order arithmetic uses:
- * The axiom of induction
- * The axiom of comprehension
- Thus we only need one more axiom to reach it. I won't go into much more detail, but in essence second-order arithmetic lets us define reals & rationals making is significantly stronger than PA.
- ### Peano Axioms as a first-order theory
- The axioms I presented earlier include a second-order axiom (the axiom of induction), as I discussed earlier. We can weaken it into a first-order theory by using an axiom schema.
- An axiom schema is simply an infinite list of axioms. So in this case, we can have a weaker version of:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- Where instead we say:
- 1. Generate a first-order formula $P$ (which we haven't generated yet)
- 2. Add the rule:
- $$P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n))$$
- This in essence makes the list of possible $P$ countable (whereas it was uncountable before).
- It turns out this limits the types of sets in PA significantly.
- Therefore the PA we defined earlier is stronger than this theory, but weaker than second-order arithmetic.
- Yes, your right the axioms are (usually) written in first-order logic (FOL).
- However, we can "cheat" by using natural language to describe our axioms (which is done in the Wikipedia article).
- After all at some point some axioms will need to be defined in natural language.
- (e.g.: If Peano Axioms are defined in FOL, then what is FOL defined with?)
- Therefore to make them "primitive notions", we simply cheat by defining them in natural language.
- ### Why do we need these axioms specifically?
- The Peano Axioms (PA) are:
- * a) 0 is a natural number
- * b) For all natural numbers $n$, $S(n)$ is a natural number
- * c) For all natural numbers $n$ & $m$, if $S(n) = S(m)$, then $n = m$
- * d) For all natural numbers $n$, $S(n) = 0$ is false
- * e) Given a set $K$ which contains $0$,
- If whenever a natural numbers $n$ is in $K$ also means $S(n)$ is in $K$,
- Then $K$ contains all natural numbers.
- So the first 2 axioms are pretty intuitive, as they're required to create a structure with multiple elements:
- * a) We have the natural number: $0$
- *"We need a starting point"*
- * b) We now have natural numbers: $0, S(0), S(S(0)), ...$
- *"We can take steps from the starting point"*
- Now at this point, the natural numbers *could* be several sets. The following are alternative systems that have yet to be disqualified, meaning the first two axioms don't describe $\mathbb{N}$ in a satisfactory way:
- 1. **Preorder-like structure:**
- $\{ 0, a, S(0) \}$ where $S(0) = S(a)$ and $S(S(0)) = 0$
- 2. **Cyclic structure:**
- $\{ 0, S(0), S(S(0)) \}$ and $S(S(S(0))) = 0$ or $\{ 0, 1, 2 \}$ are the only numbers and $2 + 1 = 0$
- 3. **Two zeros:**
- $\{ 0, a, S(0), S(a), S(S(0)), \dots \}$ where $a \neq 0$
- Graphically, we can visualize these in the following way:
- 
- These structures are successfully ruled out by the remaining axioms:
- * Axiom (c) successfully rules out (1) since $S(0) = S(a)$, but $a \neq 0$.
- We can interpret (c) as a type of linearization axiom where:
- *"There is only one path to get to a number by successive steps"*
- * Axiom (d) successfully rules out (2) since $S(S(0)) = 0$ contradicting the axiom.
- We can interpret (d) as a no-loops axiom where:
- *"There is no number whose next number is zero"*
- **(Notice this also rules out negative numbers, so it's also a no-negatives axiom)**
- * Axiom (e) intuitively means: all natural numbers can be obtained by applying $S$ to $0$.
- This fails for (3), since $a$ cannot be obtained by applying $S$ to $0$. One way to put it is:
- *"All natural numbers are obtained from 0"*
- Now, one might think: *are these axioms sufficient? Do we know if these actually are the natural numbers we think of intuitively?* The answer to both is *"we don't know"*. They seem to be sufficient for proving standard results in number theory, however whether they are *"actually the natural numbers"* is a philosophical question.
- Of course there also different axioms which can define this same structure. But these ones just happened to become standard for historical & practical reasons.
- ### Regarding the axioms of equality
- Notice that we used the notion of equality several times when defining the axioms. We used an operator $=$, and we forgot to define it.
- While we could argue that "equality is intuitive", formally it should be specified. This is what the equality axioms do.
- ### Regarding the axiom of induction
- The reason why this is a second-order statement, is actually hidden in our formulation. Notice however that we used the notion of a "set" in the definition. This is where the "second-order"-ness is coming in.
- We are saying something about "all sets", meaning we are using a quantifier over the "sets". This is what is second-order about it.
- Another formulation of the axioms where $P$ is a predicate is:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- You can change $P(x)$ to $x \in K$ to get the same definition we used earlier. Notice that $\forall P$ is a quantifier over all predicates, whereas $\forall n$ is a quantifier over all numbers.
- Having $\forall P$ is what makes it a second-order statement.
- So yes, this can be understood as having bound variables which are first-order sentences themselves.
- ### Relation to second-order arithmetic
- The axiom of induction makes the formulation close to second-order arithmetic since second-order arithmetic uses:
- * The axiom of induction
- * The axiom of comprehension
- Thus we only need one more axiom to reach it. I won't go into much more detail, but in essence second-order arithmetic lets us define reals & rationals making is significantly stronger than PA.
- ### Peano Axioms as a first-order theory
- The axioms I presented earlier include a second-order axiom (the axiom of induction), as I discussed earlier. We can weaken it into a first-order theory by using an axiom schema.
- An axiom schema is simply an infinite list of axioms. So in this case, we can have a weaker version of:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- Where instead we say:
- 1. Generate a first-order formula $P$ (which we haven't generated yet)
- 2. Add the rule:
- $$P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n))$$
- This in essence makes the list of possible $P$ countable (whereas it was uncountable before).
- It turns out this limits the types of sets in PA significantly.
- Therefore the PA we defined earlier is stronger than this theory, but weaker than second-order arithmetic.
#7: Post edited
- Yes, your right the axioms are (usually) written in first-order logic (FOL).
- However, we can "cheat" by using natural language to describe our axioms (which is done in the Wikipedia article).
- After all at some point some axioms will need to be defined in natural language.
- (e.g.: If Peano Axioms are defined in FOL, then what is FOL defined with?)
- Therefore to make them "primitive notions", we simply cheat by defining them in natural language.
- ### Why do we need these axioms specifically?
- The Peano Axioms (PA) are:
- * a) 0 is a natural number
- * b) For all natural numbers $n$, $S(n)$ is a natural number
- * c) For all natural numbers $n$ & $m$, if $S(n) = S(m)$, then $n = m$
- * d) For all natural numbers $n$, $S(n) = 0$ is false
- * e) Given a set $K$ which contains $0$,
- If whenever a natural numbers $n$ is in $K$ also means $S(n)$ is in $K$,
- Then $K$ contains all natural numbers.
- So the first 2 axioms are pretty intuitive, as they're required to create any structure with multiple elements:
- * a) We have the natural number: $0$
- *"We need a starting point"*
- * b) We now have natural numbers: $0, S(0), S(S(0)), ...$
- *"We can take steps from the starting point"*
- Now at this point, the natural numbers *could* be several sets. The following are alternative systems that have yet to be disqualified, meaning the first two axioms don't describe $\mathbb{N}$ in a satisfactory way:
- 1. **Preorder-like structure:**
- $\{ 0, a, S(0) \}$ where $S(0) = S(a)$ and $S(S(0)) = 0$
2. **Cyclic group of 3 elements:**- $\{ 0, S(0), S(S(0)) \}$ and $S(S(S(0))) = 0$ or $\{ 0, 1, 2 \}$ are the only numbers and $2 + 1 = 0$
- 3. **Two zeros:**
- $\{ 0, a, S(0), S(a), S(S(0)), \dots \}$ where $a \neq 0$
- Graphically, we can visualize these in the following way:
- 
- These structures are successfully ruled out by the remaining axioms:
- * Axiom (c) successfully rules out (1) since $S(0) = S(a)$, but $a \neq 0$.
- We can interpret (c) as a type of linearization axiom where:
- *"There is only one path to get to a number by successive steps"*
- * Axiom (d) successfully rules out (2) since $S(S(0)) = 0$ contradicting the axiom.
- We can interpret (d) as a no-loops axiom where:
- *"There is no number whose next number is zero"*
- **(Notice this also rules out negative numbers, so it's also a no-negatives axiom)**
- * Axiom (e) intuitively means: all natural numbers can be obtained by applying $S$ to $0$.
- This fails for (3), since $a$ cannot be obtained by applying $S$ to $0$. One way to put it is:
- *"All natural numbers are obtained from 0"*
- Now, one might think: *are these axioms sufficient? Do we know if these actually are the natural numbers we think of intuitively?* The answer to both is *"we don't know"*. They seem to be sufficient for proving standard results in number theory, however whether they are *"actually the natural numbers"* is a philosophical question.
- Of course there also different axioms which can define this same structure. But these ones just happened to become standard for historical & practical reasons.
- ### Regarding the axioms of equality
- Notice that we used the notion of equality several times when defining the axioms. We used an operator $=$, and we forgot to define it.
- While we could argue that "equality is intuitive", formally it should be specified. This is what the equality axioms do.
- ### Regarding the axiom of induction
- The reason why this is a second-order statement, is actually hidden in our formulation. Notice however that we used the notion of a "set" in the definition. This is where the "second-order"-ness is coming in.
- We are saying something about "all sets", meaning we are using a quantifier over the "sets". This is what is second-order about it.
- Another formulation of the axioms where $P$ is a predicate is:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- You can change $P(x)$ to $x \in K$ to get the same definition we used earlier. Notice that $\forall P$ is a quantifier over all predicates, whereas $\forall n$ is a quantifier over all numbers.
- Having $\forall P$ is what makes it a second-order statement.
- So yes, this can be understood as having bound variables which are first-order sentences themselves.
- ### Relation to second-order arithmetic
- The axiom of induction makes the formulation close to second-order arithmetic since second-order arithmetic uses:
- * The axiom of induction
- * The axiom of comprehension
- Thus we only need one more axiom to reach it. I won't go into much more detail, but in essence second-order arithmetic lets us define reals & rationals making is significantly stronger than PA.
- ### Peano Axioms as a first-order theory
- The axioms I presented earlier include a second-order axiom (the axiom of induction), as I discussed earlier. We can weaken it into a first-order theory by using an axiom schema.
- An axiom schema is simply an infinite list of axioms. So in this case, we can have a weaker version of:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- Where instead we say:
- 1. Generate a first-order formula $P$ (which we haven't generated yet)
- 2. Add the rule:
- $$P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n))$$
- This in essence makes the list of possible $P$ countable (whereas it was uncountable before).
- It turns out this limits the types of sets in PA significantly.
- Therefore the PA we defined earlier is stronger than this theory, but weaker than second-order arithmetic.
- Yes, your right the axioms are (usually) written in first-order logic (FOL).
- However, we can "cheat" by using natural language to describe our axioms (which is done in the Wikipedia article).
- After all at some point some axioms will need to be defined in natural language.
- (e.g.: If Peano Axioms are defined in FOL, then what is FOL defined with?)
- Therefore to make them "primitive notions", we simply cheat by defining them in natural language.
- ### Why do we need these axioms specifically?
- The Peano Axioms (PA) are:
- * a) 0 is a natural number
- * b) For all natural numbers $n$, $S(n)$ is a natural number
- * c) For all natural numbers $n$ & $m$, if $S(n) = S(m)$, then $n = m$
- * d) For all natural numbers $n$, $S(n) = 0$ is false
- * e) Given a set $K$ which contains $0$,
- If whenever a natural numbers $n$ is in $K$ also means $S(n)$ is in $K$,
- Then $K$ contains all natural numbers.
- So the first 2 axioms are pretty intuitive, as they're required to create any structure with multiple elements:
- * a) We have the natural number: $0$
- *"We need a starting point"*
- * b) We now have natural numbers: $0, S(0), S(S(0)), ...$
- *"We can take steps from the starting point"*
- Now at this point, the natural numbers *could* be several sets. The following are alternative systems that have yet to be disqualified, meaning the first two axioms don't describe $\mathbb{N}$ in a satisfactory way:
- 1. **Preorder-like structure:**
- $\{ 0, a, S(0) \}$ where $S(0) = S(a)$ and $S(S(0)) = 0$
- 2. **Cyclic structure:**
- $\{ 0, S(0), S(S(0)) \}$ and $S(S(S(0))) = 0$ or $\{ 0, 1, 2 \}$ are the only numbers and $2 + 1 = 0$
- 3. **Two zeros:**
- $\{ 0, a, S(0), S(a), S(S(0)), \dots \}$ where $a \neq 0$
- Graphically, we can visualize these in the following way:
- 
- These structures are successfully ruled out by the remaining axioms:
- * Axiom (c) successfully rules out (1) since $S(0) = S(a)$, but $a \neq 0$.
- We can interpret (c) as a type of linearization axiom where:
- *"There is only one path to get to a number by successive steps"*
- * Axiom (d) successfully rules out (2) since $S(S(0)) = 0$ contradicting the axiom.
- We can interpret (d) as a no-loops axiom where:
- *"There is no number whose next number is zero"*
- **(Notice this also rules out negative numbers, so it's also a no-negatives axiom)**
- * Axiom (e) intuitively means: all natural numbers can be obtained by applying $S$ to $0$.
- This fails for (3), since $a$ cannot be obtained by applying $S$ to $0$. One way to put it is:
- *"All natural numbers are obtained from 0"*
- Now, one might think: *are these axioms sufficient? Do we know if these actually are the natural numbers we think of intuitively?* The answer to both is *"we don't know"*. They seem to be sufficient for proving standard results in number theory, however whether they are *"actually the natural numbers"* is a philosophical question.
- Of course there also different axioms which can define this same structure. But these ones just happened to become standard for historical & practical reasons.
- ### Regarding the axioms of equality
- Notice that we used the notion of equality several times when defining the axioms. We used an operator $=$, and we forgot to define it.
- While we could argue that "equality is intuitive", formally it should be specified. This is what the equality axioms do.
- ### Regarding the axiom of induction
- The reason why this is a second-order statement, is actually hidden in our formulation. Notice however that we used the notion of a "set" in the definition. This is where the "second-order"-ness is coming in.
- We are saying something about "all sets", meaning we are using a quantifier over the "sets". This is what is second-order about it.
- Another formulation of the axioms where $P$ is a predicate is:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- You can change $P(x)$ to $x \in K$ to get the same definition we used earlier. Notice that $\forall P$ is a quantifier over all predicates, whereas $\forall n$ is a quantifier over all numbers.
- Having $\forall P$ is what makes it a second-order statement.
- So yes, this can be understood as having bound variables which are first-order sentences themselves.
- ### Relation to second-order arithmetic
- The axiom of induction makes the formulation close to second-order arithmetic since second-order arithmetic uses:
- * The axiom of induction
- * The axiom of comprehension
- Thus we only need one more axiom to reach it. I won't go into much more detail, but in essence second-order arithmetic lets us define reals & rationals making is significantly stronger than PA.
- ### Peano Axioms as a first-order theory
- The axioms I presented earlier include a second-order axiom (the axiom of induction), as I discussed earlier. We can weaken it into a first-order theory by using an axiom schema.
- An axiom schema is simply an infinite list of axioms. So in this case, we can have a weaker version of:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- Where instead we say:
- 1. Generate a first-order formula $P$ (which we haven't generated yet)
- 2. Add the rule:
- $$P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n))$$
- This in essence makes the list of possible $P$ countable (whereas it was uncountable before).
- It turns out this limits the types of sets in PA significantly.
- Therefore the PA we defined earlier is stronger than this theory, but weaker than second-order arithmetic.
#6: Post edited
- Yes, your right the axioms are (usually) written in first-order logic (FOL).
- However, we can "cheat" by using natural language to describe our axioms (which is done in the Wikipedia article).
- After all at some point some axioms will need to be defined in natural language.
- (e.g.: If Peano Axioms are defined in FOL, then what is FOL defined with?)
- Therefore to make them "primitive notions", we simply cheat by defining them in natural language.
- ### Why do we need these axioms specifically?
- The Peano Axioms (PA) are:
- * a) 0 is a natural number
- * b) For all natural numbers $n$, $S(n)$ is a natural number
- * c) For all natural numbers $n$ & $m$, if $S(n) = S(m)$, then $n = m$
- * d) For all natural numbers $n$, $S(n) = 0$ is false
- * e) Given a set $K$ which contains $0$,
- If whenever a natural numbers $n$ is in $K$ also means $S(n)$ is in $K$,
- Then $K$ contains all natural numbers.
- So the first 2 axioms are pretty intuitive, as they're required to create any structure with multiple elements:
- * a) We have the natural number: $0$
- *"We need a starting point"*
- * b) We now have natural numbers: $0, S(0), S(S(0)), ...$
- *"We can take steps from the starting point"*
- Now at this point, the natural numbers *could* be several sets. The following are alternative systems that have yet to be disqualified, meaning the first two axioms don't describe $\mathbb{N}$ in a satisfactory way:
- 1. **Preorder-like structure:**
- $\{ 0, a, S(0) \}$ where $S(0) = S(a)$ and $S(S(0)) = 0$
- 2. **Cyclic group of 3 elements:**
- $\{ 0, S(0), S(S(0)) \}$ and $S(S(S(0))) = 0$ or $\{ 0, 1, 2 \}$ are the only numbers and $2 + 1 = 0$
- 3. **Two zeros:**
- $\{ 0, a, S(0), S(a), S(S(0)), \dots \}$ where $a \neq 0$
- Graphically, we can visualize these in the following way:
- 
* c) This successfully rules out (1) since $S(0) = S(a)$, but $aeq 0$.- We can interpret (c) as a type of linearization axiom where:
- *"There is only one path to get to a number by successive steps"*
* d) This successfully rules out (2) since $S(S(0)) = 0$ contradicting the axiom.- We can interpret (d) as a no-loops axiom where:
- *"There is no number whose next number is zero"*
- **(Notice this also rules out negative numbers, so it's also a no-negatives axiom)**
* e) This axiom intuitively means: all natural numbers can be obtained by applying $S$ to $0$.- This fails for (3), since $a$ cannot be obtained by applying $S$ to $0$. One way to put it is:
- *"All natural numbers are obtained from 0"*
Now, one might think *are these axioms sufficient? Do we know if these actually are the natural numbers we think of intuitively?* The answer to both is *"we don't know"*. They seem to be sufficient for proving standard results in number theory, however whether they are *"actually the natural numbers"* is a philosophical question.- Of course there also different axioms which can define this same structure. But these ones just happened to become standard for historical & practical reasons.
- ### Regarding the axioms of equality
- Notice that we used the notion of equality several times when defining the axioms. We used an operator $=$, and we forgot to define it.
- While we could argue that "equality is intuitive", formally it should be specified. This is what the equality axioms do.
- ### Regarding the axiom of induction
- The reason why this is a second-order statement, is actually hidden in our formulation. Notice however that we used the notion of a "set" in the definition. This is where the "second-order"-ness is coming in.
- We are saying something about "all sets", meaning we are using a quantifier over the "sets". This is what is second-order about it.
- Another formulation of the axioms where $P$ is a predicate is:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- You can change $P(x)$ to $x \in K$ to get the same definition we used earlier. Notice that $\forall P$ is a quantifier over all predicates, whereas $\forall n$ is a quantifier over all numbers.
- So yes, this can be understood as having bound variables which are first-order sentences themselves.
- ### Relation to second-order arithmetic
- The axiom of induction makes the formulation close to second-order arithmetic since second-order arithmetic uses:
- * The axiom of induction
- * The axiom of comprehension
- Thus we only need one more axiom to reach it. I won't go into much more detail, but in essence second-order arithmetic lets us define reals & rationals making is significantly stronger than PA.
- ### Peano Axioms as a first-order theory
- The axioms I presented earlier include a second-order axiom (the axiom of induction), as I discussed earlier. We can weaken it into a first-order theory by using an axiom schema.
- An axiom schema is simply an infinite list of axioms. So in this case, we can have a weaker version of:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- Where instead we say:
- 1. Generate a first-order formula $P$ (which we haven't generated yet)
- 2. Add the rule:
- $$P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n))$$
- This in essence makes the list of possible $P$ countable (whereas it was uncountable before).
- It turns out this limits the types of sets in PA significantly.
Therefore the PA we defined, stronger than this theory, but weaker than second-order arithmetic.
- Yes, your right the axioms are (usually) written in first-order logic (FOL).
- However, we can "cheat" by using natural language to describe our axioms (which is done in the Wikipedia article).
- After all at some point some axioms will need to be defined in natural language.
- (e.g.: If Peano Axioms are defined in FOL, then what is FOL defined with?)
- Therefore to make them "primitive notions", we simply cheat by defining them in natural language.
- ### Why do we need these axioms specifically?
- The Peano Axioms (PA) are:
- * a) 0 is a natural number
- * b) For all natural numbers $n$, $S(n)$ is a natural number
- * c) For all natural numbers $n$ & $m$, if $S(n) = S(m)$, then $n = m$
- * d) For all natural numbers $n$, $S(n) = 0$ is false
- * e) Given a set $K$ which contains $0$,
- If whenever a natural numbers $n$ is in $K$ also means $S(n)$ is in $K$,
- Then $K$ contains all natural numbers.
- So the first 2 axioms are pretty intuitive, as they're required to create any structure with multiple elements:
- * a) We have the natural number: $0$
- *"We need a starting point"*
- * b) We now have natural numbers: $0, S(0), S(S(0)), ...$
- *"We can take steps from the starting point"*
- Now at this point, the natural numbers *could* be several sets. The following are alternative systems that have yet to be disqualified, meaning the first two axioms don't describe $\mathbb{N}$ in a satisfactory way:
- 1. **Preorder-like structure:**
- $\{ 0, a, S(0) \}$ where $S(0) = S(a)$ and $S(S(0)) = 0$
- 2. **Cyclic group of 3 elements:**
- $\{ 0, S(0), S(S(0)) \}$ and $S(S(S(0))) = 0$ or $\{ 0, 1, 2 \}$ are the only numbers and $2 + 1 = 0$
- 3. **Two zeros:**
- $\{ 0, a, S(0), S(a), S(S(0)), \dots \}$ where $a \neq 0$
- Graphically, we can visualize these in the following way:
- 
- These structures are successfully ruled out by the remaining axioms:
- * Axiom (c) successfully rules out (1) since $S(0) = S(a)$, but $a
- eq 0$.
- We can interpret (c) as a type of linearization axiom where:
- *"There is only one path to get to a number by successive steps"*
- * Axiom (d) successfully rules out (2) since $S(S(0)) = 0$ contradicting the axiom.
- We can interpret (d) as a no-loops axiom where:
- *"There is no number whose next number is zero"*
- **(Notice this also rules out negative numbers, so it's also a no-negatives axiom)**
- * Axiom (e) intuitively means: all natural numbers can be obtained by applying $S$ to $0$.
- This fails for (3), since $a$ cannot be obtained by applying $S$ to $0$. One way to put it is:
- *"All natural numbers are obtained from 0"*
- Now, one might think: *are these axioms sufficient? Do we know if these actually are the natural numbers we think of intuitively?* The answer to both is *"we don't know"*. They seem to be sufficient for proving standard results in number theory, however whether they are *"actually the natural numbers"* is a philosophical question.
- Of course there also different axioms which can define this same structure. But these ones just happened to become standard for historical & practical reasons.
- ### Regarding the axioms of equality
- Notice that we used the notion of equality several times when defining the axioms. We used an operator $=$, and we forgot to define it.
- While we could argue that "equality is intuitive", formally it should be specified. This is what the equality axioms do.
- ### Regarding the axiom of induction
- The reason why this is a second-order statement, is actually hidden in our formulation. Notice however that we used the notion of a "set" in the definition. This is where the "second-order"-ness is coming in.
- We are saying something about "all sets", meaning we are using a quantifier over the "sets". This is what is second-order about it.
- Another formulation of the axioms where $P$ is a predicate is:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- You can change $P(x)$ to $x \in K$ to get the same definition we used earlier. Notice that $\forall P$ is a quantifier over all predicates, whereas $\forall n$ is a quantifier over all numbers.
- Having $\forall P$ is what makes it a second-order statement.
- So yes, this can be understood as having bound variables which are first-order sentences themselves.
- ### Relation to second-order arithmetic
- The axiom of induction makes the formulation close to second-order arithmetic since second-order arithmetic uses:
- * The axiom of induction
- * The axiom of comprehension
- Thus we only need one more axiom to reach it. I won't go into much more detail, but in essence second-order arithmetic lets us define reals & rationals making is significantly stronger than PA.
- ### Peano Axioms as a first-order theory
- The axioms I presented earlier include a second-order axiom (the axiom of induction), as I discussed earlier. We can weaken it into a first-order theory by using an axiom schema.
- An axiom schema is simply an infinite list of axioms. So in this case, we can have a weaker version of:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- Where instead we say:
- 1. Generate a first-order formula $P$ (which we haven't generated yet)
- 2. Add the rule:
- $$P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n))$$
- This in essence makes the list of possible $P$ countable (whereas it was uncountable before).
- It turns out this limits the types of sets in PA significantly.
- Therefore the PA we defined earlier is stronger than this theory, but weaker than second-order arithmetic.
#5: Post edited
- Yes, your right the axioms are (usually) written in first-order logic (FOL).
- However, we can "cheat" by using natural language to describe our axioms (which is done in the Wikipedia article).
- After all at some point some axioms will need to be defined in natural language.
- (e.g.: If Peano Axioms are defined in FOL, then what is FOL defined with?)
- Therefore to make them "primitive notions", we simply cheat by defining them in natural language.
- ### Why do we need these axioms specifically?
- The Peano Axioms (PA) are:
- * a) 0 is a natural number
- * b) For all natural numbers $n$, $S(n)$ is a natural number
- * c) For all natural numbers $n$ & $m$, if $S(n) = S(m)$, then $n = m$
- * d) For all natural numbers $n$, $S(n) = 0$ is false
- * e) Given a set $K$ which contains $0$,
- If whenever a natural numbers $n$ is in $K$ also means $S(n)$ is in $K$,
- Then $K$ contains all natural numbers.
- So the first 2 axioms are pretty intuitive, as they're required to create any structure with multiple elements:
- * a) We have the natural number: $0$
- *"We need a starting point"*
- * b) We now have natural numbers: $0, S(0), S(S(0)), ...$
- *"We can take steps from the starting point"*
Now at this point, the natural numbers *could* be several sets. The following are alternative systems that have yet to be disqualified, meaning our axioms don't describe $\mathbb{N}$ in a satisfactory way:- 1. **Preorder-like structure:**
- $\{ 0, a, S(0) \}$ where $S(0) = S(a)$ and $S(S(0)) = 0$
- 2. **Cyclic group of 3 elements:**
- $\{ 0, S(0), S(S(0)) \}$ and $S(S(S(0))) = 0$ or $\{ 0, 1, 2 \}$ are the only numbers and $2 + 1 = 0$
- 3. **Two zeros:**
$\{ 0, a, S(0), S(a), S(S(0)), \dots \}$- Graphically, we can visualize these in the following way:
- 
- * c) This successfully rules out (1) since $S(0) = S(a)$, but $a \neq 0$.
- We can interpret (c) as a type of linearization axiom where:
- *"There is only one path to get to a number by successive steps"*
- * d) This successfully rules out (2) since $S(S(0)) = 0$ contradicting the axiom.
- We can interpret (d) as a no-loops axiom where:
- *"There is no number whose next number is zero"*
- **(Notice this also rules out negative numbers, so it's also a no-negatives axiom)**
- * e) This axiom intuitively means: all natural numbers can be obtained by applying $S$ to $0$.
- This fails for (3), since $a$ cannot be obtained by applying $S$ to $0$. One way to put it is:
- *"All natural numbers are obtained from 0"*
- Now, one might think *are these axioms sufficient? Do we know if these actually are the natural numbers we think of intuitively?* The answer to both is *"we don't know"*. They seem to be sufficient for proving standard results in number theory, however whether they are *"actually the natural numbers"* is a philosophical question.
- Of course there also different axioms which can define this same structure. But these ones just happened to become standard for historical & practical reasons.
- ### Regarding the axioms of equality
- Notice that we used the notion of equality several times when defining the axioms. We used an operator $=$, and we forgot to define it.
- While we could argue that "equality is intuitive", formally it should be specified. This is what the equality axioms do.
- ### Regarding the axiom of induction
- The reason why this is a second-order statement, is actually hidden in our formulation. Notice however that we used the notion of a "set" in the definition. This is where the "second-order"-ness is coming in.
- We are saying something about "all sets", meaning we are using a quantifier over the "sets". This is what is second-order about it.
- Another formulation of the axioms where $P$ is a predicate is:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- You can change $P(x)$ to $x \in K$ to get the same definition we used earlier. Notice that $\forall P$ is a quantifier over all predicates, whereas $\forall n$ is a quantifier over all numbers.
- So yes, this can be understood as having bound variables which are first-order sentences themselves.
- ### Relation to second-order arithmetic
- The axiom of induction makes the formulation close to second-order arithmetic since second-order arithmetic uses:
- * The axiom of induction
- * The axiom of comprehension
- Thus we only need one more axiom to reach it. I won't go into much more detail, but in essence second-order arithmetic lets us define reals & rationals making is significantly stronger than PA.
- ### Peano Axioms as a first-order theory
- The axioms I presented earlier include a second-order axiom (the axiom of induction), as I discussed earlier. We can weaken it into a first-order theory by using an axiom schema.
- An axiom schema is simply an infinite list of axioms. So in this case, we can have a weaker version of:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- Where instead we say:
- 1. Generate a first-order formula $P$ (which we haven't generated yet)
- 2. Add the rule:
- $$P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n))$$
- This in essence makes the list of possible $P$ countable (whereas it was uncountable before).
- It turns out this limits the types of sets in PA significantly.
- Therefore the PA we defined, stronger than this theory, but weaker than second-order arithmetic.
- Yes, your right the axioms are (usually) written in first-order logic (FOL).
- However, we can "cheat" by using natural language to describe our axioms (which is done in the Wikipedia article).
- After all at some point some axioms will need to be defined in natural language.
- (e.g.: If Peano Axioms are defined in FOL, then what is FOL defined with?)
- Therefore to make them "primitive notions", we simply cheat by defining them in natural language.
- ### Why do we need these axioms specifically?
- The Peano Axioms (PA) are:
- * a) 0 is a natural number
- * b) For all natural numbers $n$, $S(n)$ is a natural number
- * c) For all natural numbers $n$ & $m$, if $S(n) = S(m)$, then $n = m$
- * d) For all natural numbers $n$, $S(n) = 0$ is false
- * e) Given a set $K$ which contains $0$,
- If whenever a natural numbers $n$ is in $K$ also means $S(n)$ is in $K$,
- Then $K$ contains all natural numbers.
- So the first 2 axioms are pretty intuitive, as they're required to create any structure with multiple elements:
- * a) We have the natural number: $0$
- *"We need a starting point"*
- * b) We now have natural numbers: $0, S(0), S(S(0)), ...$
- *"We can take steps from the starting point"*
- Now at this point, the natural numbers *could* be several sets. The following are alternative systems that have yet to be disqualified, meaning the first two axioms don't describe $\mathbb{N}$ in a satisfactory way:
- 1. **Preorder-like structure:**
- $\{ 0, a, S(0) \}$ where $S(0) = S(a)$ and $S(S(0)) = 0$
- 2. **Cyclic group of 3 elements:**
- $\{ 0, S(0), S(S(0)) \}$ and $S(S(S(0))) = 0$ or $\{ 0, 1, 2 \}$ are the only numbers and $2 + 1 = 0$
- 3. **Two zeros:**
- $\{ 0, a, S(0), S(a), S(S(0)), \dots \}$ where $a \neq 0$
- Graphically, we can visualize these in the following way:
- 
- * c) This successfully rules out (1) since $S(0) = S(a)$, but $a \neq 0$.
- We can interpret (c) as a type of linearization axiom where:
- *"There is only one path to get to a number by successive steps"*
- * d) This successfully rules out (2) since $S(S(0)) = 0$ contradicting the axiom.
- We can interpret (d) as a no-loops axiom where:
- *"There is no number whose next number is zero"*
- **(Notice this also rules out negative numbers, so it's also a no-negatives axiom)**
- * e) This axiom intuitively means: all natural numbers can be obtained by applying $S$ to $0$.
- This fails for (3), since $a$ cannot be obtained by applying $S$ to $0$. One way to put it is:
- *"All natural numbers are obtained from 0"*
- Now, one might think *are these axioms sufficient? Do we know if these actually are the natural numbers we think of intuitively?* The answer to both is *"we don't know"*. They seem to be sufficient for proving standard results in number theory, however whether they are *"actually the natural numbers"* is a philosophical question.
- Of course there also different axioms which can define this same structure. But these ones just happened to become standard for historical & practical reasons.
- ### Regarding the axioms of equality
- Notice that we used the notion of equality several times when defining the axioms. We used an operator $=$, and we forgot to define it.
- While we could argue that "equality is intuitive", formally it should be specified. This is what the equality axioms do.
- ### Regarding the axiom of induction
- The reason why this is a second-order statement, is actually hidden in our formulation. Notice however that we used the notion of a "set" in the definition. This is where the "second-order"-ness is coming in.
- We are saying something about "all sets", meaning we are using a quantifier over the "sets". This is what is second-order about it.
- Another formulation of the axioms where $P$ is a predicate is:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- You can change $P(x)$ to $x \in K$ to get the same definition we used earlier. Notice that $\forall P$ is a quantifier over all predicates, whereas $\forall n$ is a quantifier over all numbers.
- So yes, this can be understood as having bound variables which are first-order sentences themselves.
- ### Relation to second-order arithmetic
- The axiom of induction makes the formulation close to second-order arithmetic since second-order arithmetic uses:
- * The axiom of induction
- * The axiom of comprehension
- Thus we only need one more axiom to reach it. I won't go into much more detail, but in essence second-order arithmetic lets us define reals & rationals making is significantly stronger than PA.
- ### Peano Axioms as a first-order theory
- The axioms I presented earlier include a second-order axiom (the axiom of induction), as I discussed earlier. We can weaken it into a first-order theory by using an axiom schema.
- An axiom schema is simply an infinite list of axioms. So in this case, we can have a weaker version of:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- Where instead we say:
- 1. Generate a first-order formula $P$ (which we haven't generated yet)
- 2. Add the rule:
- $$P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n))$$
- This in essence makes the list of possible $P$ countable (whereas it was uncountable before).
- It turns out this limits the types of sets in PA significantly.
- Therefore the PA we defined, stronger than this theory, but weaker than second-order arithmetic.
#4: Post edited
- Yes, your right the axioms are (usually) written in first-order logic (FOL).
- However, we can "cheat" by using natural language to describe our axioms (which is done in the Wikipedia article).
- After all at some point some axioms will need to be defined in natural language.
- (e.g.: If Peano Axioms are defined in FOL, then what is FOL defined with?)
- Therefore to make them "primitive notions", we simply cheat by defining them in natural language.
- ### Why do we need these axioms specifically?
The axioms of Peano Axioms (PA) are:- * a) 0 is a natural number
- * b) For all natural numbers $n$, $S(n)$ is a natural number
- * c) For all natural numbers $n$ & $m$, if $S(n) = S(m)$, then $n = m$
- * d) For all natural numbers $n$, $S(n) = 0$ is false
- * e) Given a set $K$ which contains $0$,
- If whenever a natural numbers $n$ is in $K$ also means $S(n)$ is in $K$,
- Then $K$ contains all natural numbers.
- So the first 2 axioms are pretty intuitive, as they're required to create any structure with multiple elements:
- * a) We have the natural number: $0$
- *"We need a starting point"*
- * b) We now have natural numbers: $0, S(0), S(S(0)), ...$
- *"We can take steps from the starting point"*
- Now at this point, the natural numbers *could* be several sets. The following are alternative systems that have yet to be disqualified, meaning our axioms don't describe $\mathbb{N}$ in a satisfactory way:
- 1. **Preorder-like structure:**
- $\{ 0, a, S(0) \}$ where $S(0) = S(a)$ and $S(S(0)) = 0$
- 2. **Cyclic group of 3 elements:**
- $\{ 0, S(0), S(S(0)) \}$ and $S(S(S(0))) = 0$ or $\{ 0, 1, 2 \}$ are the only numbers and $2 + 1 = 0$
- 3. **Two zeros:**
- $\{ 0, a, S(0), S(a), S(S(0)), \dots \}$
- Graphically, we can visualize these in the following way:
- 
- * c) This successfully rules out (1) since $S(0) = S(a)$, but $a \neq 0$.
- We can interpret (c) as a type of linearization axiom where:
- *"There is only one path to get to a number by successive steps"*
- * d) This successfully rules out (2) since $S(S(0)) = 0$ contradicting the axiom.
- We can interpret (d) as a no-loops axiom where:
- *"There is no number whose next number is zero"*
- **(Notice this also rules out negative numbers, so it's also a no-negatives axiom)**
- * e) This axiom intuitively means: all natural numbers can be obtained by applying $S$ to $0$.
- This fails for (3), since $a$ cannot be obtained by applying $S$ to $0$. One way to put it is:
- *"All natural numbers are obtained from 0"*
- Now, one might think *are these axioms sufficient? Do we know if these actually are the natural numbers we think of intuitively?* The answer to both is *"we don't know"*. They seem to be sufficient for proving standard results in number theory, however whether they are *"actually the natural numbers"* is a philosophical question.
- Of course there also different axioms which can define this same structure. But these ones just happened to become standard for historical & practical reasons.
- ### Regarding the axioms of equality
- Notice that we used the notion of equality several times when defining the axioms. We used an operator $=$, and we forgot to define it.
- While we could argue that "equality is intuitive", formally it should be specified. This is what the equality axioms do.
- ### Regarding the axiom of induction
- The reason why this is a second-order statement, is actually hidden in our formulation. Notice however that we used the notion of a "set" in the definition. This is where the "second-order"-ness is coming in.
- We are saying something about "all sets", meaning we are using a quantifier over the "sets". This is what is second-order about it.
- Another formulation of the axioms where $P$ is a predicate is:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- You can change $P(x)$ to $x \in K$ to get the same definition we used earlier. Notice that $\forall P$ is a quantifier over all predicates, whereas $\forall n$ is a quantifier over all numbers.
- So yes, this can be understood as having bound variables which are first-order sentences themselves.
- ### Relation to second-order arithmetic
- The axiom of induction makes the formulation close to second-order arithmetic since second-order arithmetic uses:
- * The axiom of induction
- * The axiom of comprehension
- Thus we only need one more axiom to reach it. I won't go into much more detail, but in essence second-order arithmetic lets us define reals & rationals making is significantly stronger than PA.
- ### Peano Axioms as a first-order theory
- The axioms I presented earlier include a second-order axiom (the axiom of induction), as I discussed earlier. We can weaken it into a first-order theory by using an axiom schema.
- An axiom schema is simply an infinite list of axioms. So in this case, we can have a weaker version of:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- Where instead we say:
- 1. Generate a first-order formula $P$ (which we haven't generated yet)
- 2. Add the rule:
- $$P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n))$$
- This in essence makes the list of possible $P$ countable (whereas it was uncountable before).
- It turns out this limits the types of sets in PA significantly.
- Therefore the PA we defined, stronger than this theory, but weaker than second-order arithmetic.
- Yes, your right the axioms are (usually) written in first-order logic (FOL).
- However, we can "cheat" by using natural language to describe our axioms (which is done in the Wikipedia article).
- After all at some point some axioms will need to be defined in natural language.
- (e.g.: If Peano Axioms are defined in FOL, then what is FOL defined with?)
- Therefore to make them "primitive notions", we simply cheat by defining them in natural language.
- ### Why do we need these axioms specifically?
- The Peano Axioms (PA) are:
- * a) 0 is a natural number
- * b) For all natural numbers $n$, $S(n)$ is a natural number
- * c) For all natural numbers $n$ & $m$, if $S(n) = S(m)$, then $n = m$
- * d) For all natural numbers $n$, $S(n) = 0$ is false
- * e) Given a set $K$ which contains $0$,
- If whenever a natural numbers $n$ is in $K$ also means $S(n)$ is in $K$,
- Then $K$ contains all natural numbers.
- So the first 2 axioms are pretty intuitive, as they're required to create any structure with multiple elements:
- * a) We have the natural number: $0$
- *"We need a starting point"*
- * b) We now have natural numbers: $0, S(0), S(S(0)), ...$
- *"We can take steps from the starting point"*
- Now at this point, the natural numbers *could* be several sets. The following are alternative systems that have yet to be disqualified, meaning our axioms don't describe $\mathbb{N}$ in a satisfactory way:
- 1. **Preorder-like structure:**
- $\{ 0, a, S(0) \}$ where $S(0) = S(a)$ and $S(S(0)) = 0$
- 2. **Cyclic group of 3 elements:**
- $\{ 0, S(0), S(S(0)) \}$ and $S(S(S(0))) = 0$ or $\{ 0, 1, 2 \}$ are the only numbers and $2 + 1 = 0$
- 3. **Two zeros:**
- $\{ 0, a, S(0), S(a), S(S(0)), \dots \}$
- Graphically, we can visualize these in the following way:
- 
- * c) This successfully rules out (1) since $S(0) = S(a)$, but $a \neq 0$.
- We can interpret (c) as a type of linearization axiom where:
- *"There is only one path to get to a number by successive steps"*
- * d) This successfully rules out (2) since $S(S(0)) = 0$ contradicting the axiom.
- We can interpret (d) as a no-loops axiom where:
- *"There is no number whose next number is zero"*
- **(Notice this also rules out negative numbers, so it's also a no-negatives axiom)**
- * e) This axiom intuitively means: all natural numbers can be obtained by applying $S$ to $0$.
- This fails for (3), since $a$ cannot be obtained by applying $S$ to $0$. One way to put it is:
- *"All natural numbers are obtained from 0"*
- Now, one might think *are these axioms sufficient? Do we know if these actually are the natural numbers we think of intuitively?* The answer to both is *"we don't know"*. They seem to be sufficient for proving standard results in number theory, however whether they are *"actually the natural numbers"* is a philosophical question.
- Of course there also different axioms which can define this same structure. But these ones just happened to become standard for historical & practical reasons.
- ### Regarding the axioms of equality
- Notice that we used the notion of equality several times when defining the axioms. We used an operator $=$, and we forgot to define it.
- While we could argue that "equality is intuitive", formally it should be specified. This is what the equality axioms do.
- ### Regarding the axiom of induction
- The reason why this is a second-order statement, is actually hidden in our formulation. Notice however that we used the notion of a "set" in the definition. This is where the "second-order"-ness is coming in.
- We are saying something about "all sets", meaning we are using a quantifier over the "sets". This is what is second-order about it.
- Another formulation of the axioms where $P$ is a predicate is:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- You can change $P(x)$ to $x \in K$ to get the same definition we used earlier. Notice that $\forall P$ is a quantifier over all predicates, whereas $\forall n$ is a quantifier over all numbers.
- So yes, this can be understood as having bound variables which are first-order sentences themselves.
- ### Relation to second-order arithmetic
- The axiom of induction makes the formulation close to second-order arithmetic since second-order arithmetic uses:
- * The axiom of induction
- * The axiom of comprehension
- Thus we only need one more axiom to reach it. I won't go into much more detail, but in essence second-order arithmetic lets us define reals & rationals making is significantly stronger than PA.
- ### Peano Axioms as a first-order theory
- The axioms I presented earlier include a second-order axiom (the axiom of induction), as I discussed earlier. We can weaken it into a first-order theory by using an axiom schema.
- An axiom schema is simply an infinite list of axioms. So in this case, we can have a weaker version of:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- Where instead we say:
- 1. Generate a first-order formula $P$ (which we haven't generated yet)
- 2. Add the rule:
- $$P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n))$$
- This in essence makes the list of possible $P$ countable (whereas it was uncountable before).
- It turns out this limits the types of sets in PA significantly.
- Therefore the PA we defined, stronger than this theory, but weaker than second-order arithmetic.
#3: Post edited
- Yes, your right the axioms are (usually) written in first-order logic (FOL).
- However, we can "cheat" by using natural language to describe our axioms (which is done in the Wikipedia article).
- After all at some point some axioms will need to be defined in natural language.
- (e.g.: If Peano Axioms are defined in FOL, then what is FOL defined with?)
- Therefore to make them "primitive notions", we simply cheat by defining them in natural language.
### What are the Peano Axioms?- The axioms of Peano Axioms (PA) are:
- * a) 0 is a natural number
- * b) For all natural numbers $n$, $S(n)$ is a natural number
- * c) For all natural numbers $n$ & $m$, if $S(n) = S(m)$, then $n = m$
- * d) For all natural numbers $n$, $S(n) = 0$ is false
- * e) Given a set $K$ which contains $0$,
- If whenever a natural numbers $n$ is in $K$ also means $S(n)$ is in $K$,
- Then $K$ contains all natural numbers.
- So the first 2 axioms are pretty intuitive, as they're required to create any structure with multiple elements:
- * a) We have the natural number: $0$
- *"We need a starting point"*
- * b) We now have natural numbers: $0, S(0), S(S(0)), ...$
- *"We can take steps from the starting point"*
- Now at this point, the natural numbers *could* be several sets. The following are alternative systems that have yet to be disqualified, meaning our axioms don't describe $\mathbb{N}$ in a satisfactory way:
- 1. **Preorder-like structure:**
- $\{ 0, a, S(0) \}$ where $S(0) = S(a)$ and $S(S(0)) = 0$
- 2. **Cyclic group of 3 elements:**
- $\{ 0, S(0), S(S(0)) \}$ and $S(S(S(0))) = 0$ or $\{ 0, 1, 2 \}$ are the only numbers and $2 + 1 = 0$
- 3. **Two zeros:**
- $\{ 0, a, S(0), S(a), S(S(0)), \dots \}$
- Graphically, we can visualize these in the following way:
- 
- * c) This successfully rules out (1) since $S(0) = S(a)$, but $a \neq 0$.
- We can interpret (c) as a type of linearization axiom where:
- *"There is only one path to get to a number by successive steps"*
- * d) This successfully rules out (2) since $S(S(0)) = 0$ contradicting the axiom.
- We can interpret (d) as a no-loops axiom where:
- *"There is no number whose next number is zero"*
- **(Notice this also rules out negative numbers, so it's also a no-negatives axiom)**
- * e) This axiom intuitively means: all natural numbers can be obtained by applying $S$ to $0$.
- This fails for (3), since $a$ cannot be obtained by applying $S$ to $0$. One way to put it is:
- *"All natural numbers are obtained from 0"*
- Now, one might think *are these axioms sufficient? Do we know if these actually are the natural numbers we think of intuitively?* The answer to both is *"we don't know"*. They seem to be sufficient for proving standard results in number theory, however whether they are *"actually the natural numbers"* is a philosophical question.
- ### Regarding the axioms of equality
- Notice that we used the notion of equality several times when defining the axioms. We used an operator $=$, and we forgot to define it.
- While we could argue that "equality is intuitive", formally it should be specified. This is what the equality axioms do.
- ### Regarding the axiom of induction
- The reason why this is a second-order statement, is actually hidden in our formulation. Notice however that we used the notion of a "set" in the definition. This is where the "second-order"-ness is coming in.
- We are saying something about "all sets", meaning we are using a quantifier over the "sets". This is what is second-order about it.
- Another formulation of the axioms where $P$ is a predicate is:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- You can change $P(x)$ to $x \in K$ to get the same definition we used earlier. Notice that $\forall P$ is a quantifier over all predicates, whereas $\forall n$ is a quantifier over all numbers.
- So yes, this can be understood as having bound variables which are first-order sentences themselves.
- ### Relation to second-order arithmetic
- The axiom of induction makes the formulation close to second-order arithmetic since second-order arithmetic uses:
- * The axiom of induction
- * The axiom of comprehension
- Thus we only need one more axiom to reach it. I won't go into much more detail, but in essence second-order arithmetic lets us define reals & rationals making is significantly stronger than PA.
- ### Peano Axioms as a first-order theory
- The axioms I presented earlier include a second-order axiom (the axiom of induction), as I discussed earlier. We can weaken it into a first-order theory by using an axiom schema.
- An axiom schema is simply an infinite list of axioms. So in this case, we can have a weaker version of:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- Where instead we say:
- 1. Generate a first-order formula $P$ (which we haven't generated yet)
- 2. Add the rule:
- $$P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n))$$
- This in essence makes the list of possible $P$ countable (whereas it was uncountable before).
- It turns out this limits the types of sets in PA significantly.
- Therefore the PA we defined, stronger than this theory, but weaker than second-order arithmetic.
- Yes, your right the axioms are (usually) written in first-order logic (FOL).
- However, we can "cheat" by using natural language to describe our axioms (which is done in the Wikipedia article).
- After all at some point some axioms will need to be defined in natural language.
- (e.g.: If Peano Axioms are defined in FOL, then what is FOL defined with?)
- Therefore to make them "primitive notions", we simply cheat by defining them in natural language.
- ### Why do we need these axioms specifically?
- The axioms of Peano Axioms (PA) are:
- * a) 0 is a natural number
- * b) For all natural numbers $n$, $S(n)$ is a natural number
- * c) For all natural numbers $n$ & $m$, if $S(n) = S(m)$, then $n = m$
- * d) For all natural numbers $n$, $S(n) = 0$ is false
- * e) Given a set $K$ which contains $0$,
- If whenever a natural numbers $n$ is in $K$ also means $S(n)$ is in $K$,
- Then $K$ contains all natural numbers.
- So the first 2 axioms are pretty intuitive, as they're required to create any structure with multiple elements:
- * a) We have the natural number: $0$
- *"We need a starting point"*
- * b) We now have natural numbers: $0, S(0), S(S(0)), ...$
- *"We can take steps from the starting point"*
- Now at this point, the natural numbers *could* be several sets. The following are alternative systems that have yet to be disqualified, meaning our axioms don't describe $\mathbb{N}$ in a satisfactory way:
- 1. **Preorder-like structure:**
- $\{ 0, a, S(0) \}$ where $S(0) = S(a)$ and $S(S(0)) = 0$
- 2. **Cyclic group of 3 elements:**
- $\{ 0, S(0), S(S(0)) \}$ and $S(S(S(0))) = 0$ or $\{ 0, 1, 2 \}$ are the only numbers and $2 + 1 = 0$
- 3. **Two zeros:**
- $\{ 0, a, S(0), S(a), S(S(0)), \dots \}$
- Graphically, we can visualize these in the following way:
- 
- * c) This successfully rules out (1) since $S(0) = S(a)$, but $a \neq 0$.
- We can interpret (c) as a type of linearization axiom where:
- *"There is only one path to get to a number by successive steps"*
- * d) This successfully rules out (2) since $S(S(0)) = 0$ contradicting the axiom.
- We can interpret (d) as a no-loops axiom where:
- *"There is no number whose next number is zero"*
- **(Notice this also rules out negative numbers, so it's also a no-negatives axiom)**
- * e) This axiom intuitively means: all natural numbers can be obtained by applying $S$ to $0$.
- This fails for (3), since $a$ cannot be obtained by applying $S$ to $0$. One way to put it is:
- *"All natural numbers are obtained from 0"*
- Now, one might think *are these axioms sufficient? Do we know if these actually are the natural numbers we think of intuitively?* The answer to both is *"we don't know"*. They seem to be sufficient for proving standard results in number theory, however whether they are *"actually the natural numbers"* is a philosophical question.
- Of course there also different axioms which can define this same structure. But these ones just happened to become standard for historical & practical reasons.
- ### Regarding the axioms of equality
- Notice that we used the notion of equality several times when defining the axioms. We used an operator $=$, and we forgot to define it.
- While we could argue that "equality is intuitive", formally it should be specified. This is what the equality axioms do.
- ### Regarding the axiom of induction
- The reason why this is a second-order statement, is actually hidden in our formulation. Notice however that we used the notion of a "set" in the definition. This is where the "second-order"-ness is coming in.
- We are saying something about "all sets", meaning we are using a quantifier over the "sets". This is what is second-order about it.
- Another formulation of the axioms where $P$ is a predicate is:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- You can change $P(x)$ to $x \in K$ to get the same definition we used earlier. Notice that $\forall P$ is a quantifier over all predicates, whereas $\forall n$ is a quantifier over all numbers.
- So yes, this can be understood as having bound variables which are first-order sentences themselves.
- ### Relation to second-order arithmetic
- The axiom of induction makes the formulation close to second-order arithmetic since second-order arithmetic uses:
- * The axiom of induction
- * The axiom of comprehension
- Thus we only need one more axiom to reach it. I won't go into much more detail, but in essence second-order arithmetic lets us define reals & rationals making is significantly stronger than PA.
- ### Peano Axioms as a first-order theory
- The axioms I presented earlier include a second-order axiom (the axiom of induction), as I discussed earlier. We can weaken it into a first-order theory by using an axiom schema.
- An axiom schema is simply an infinite list of axioms. So in this case, we can have a weaker version of:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- Where instead we say:
- 1. Generate a first-order formula $P$ (which we haven't generated yet)
- 2. Add the rule:
- $$P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n))$$
- This in essence makes the list of possible $P$ countable (whereas it was uncountable before).
- It turns out this limits the types of sets in PA significantly.
- Therefore the PA we defined, stronger than this theory, but weaker than second-order arithmetic.
#2: Post edited
- Yes, your right the axioms are (usually) written in first-order logic (FOL).
- However, we can "cheat" by using natural language to describe our axioms (which is done in the Wikipedia article).
- After all at some point some axioms will need to be defined in natural language.
- (e.g.: If Peano Axioms are defined in FOL, then what is FOL defined with?)
- Therefore to make them "primitive notions", we simply cheat by defining them in natural language.
- ### What are the Peano Axioms?
- The axioms of Peano Axioms (PA) are:
- * a) 0 is a natural number
- * b) For all natural numbers $n$, $S(n)$ is a natural number
- * c) For all natural numbers $n$ & $m$, if $S(n) = S(m)$, then $n = m$
- * d) For all natural numbers $n$, $S(n) = 0$ is false
- * e) Given a set $K$ which contains $0$,
- If whenever a natural numbers $n$ is in $K$ also means $S(n)$ is in $K$,
- Then $K$ contains all natural numbers.
- So the first 2 axioms are pretty intuitive, as they're required to create any structure with multiple elements:
- * a) We have the natural number: $0$
- *"We need a starting point"*
- * b) We now have natural numbers: $0, S(0), S(S(0)), ...$
- *"We can take steps from the starting point"*
- Now at this point, the natural numbers *could* be several sets. The following are alternative systems that have yet to be disqualified, meaning our axioms don't describe $\mathbb{N}$ in a satisfactory way:
- 1. **Preorder-like structure:**
- $\{ 0, a, S(0) \}$ where $S(0) = S(a)$ and $S(S(0)) = 0$
- 2. **Cyclic group of 3 elements:**
- $\{ 0, S(0), S(S(0)) \}$ and $S(S(S(0))) = 0$ or $\{ 0, 1, 2 \}$ are the only numbers and $2 + 1 = 0$
- 3. **Two zeros:**
- $\{ 0, a, S(0), S(a), S(S(0)), \dots \}$
- Graphically, we can visualize these in the following way:
- 
- * c) This successfully rules out (1) since $S(0) = S(a)$, but $a \neq 0$.
- We can interpret (c) as a type of linearization axiom where:
- *"There is only one path to get to a number by successive steps"*
- * d) This successfully rules out (2) since $S(S(0)) = 0$ contradicting the axiom.
- We can interpret (d) as a no-loops axiom where:
- *"There is no number whose next number is zero"*
- **(Notice this also rules out negative numbers, so it's also a no-negatives axiom)**
- * e) This axiom intuitively means: all natural numbers can be obtained by applying $S$ to $0$.
- This fails for (3), since $a$ cannot be obtained by applying $S$ to $0$. One way to put it is:
- *"All natural numbers are obtained from 0"*
- Now, one might think *are these axioms sufficient? Do we know if these actually are the natural numbers we think of intuitively?* The answer to both is *"we don't know"*. They seem to be sufficient for proving standard results in number theory, however whether they are *"actually the natural numbers"* is a philosophical question.
- ### Regarding the axioms of equality
- Notice that we used the notion of equality several times when defining the axioms. We used an operator $=$, and we forgot to define it.
- While we could argue that "equality is intuitive", formally it should be specified. This is what the equality axioms do.
- ### Regarding the axiom of induction
- The reason why this is a second-order statement, is actually hidden in our formulation. Notice however that we used the notion of a "set" in the definition. This is where the "second-order"-ness is coming in.
- We are saying something about "all sets", meaning we are using a quantifier over the "sets". This is what is second-order about it.
- Another formulation of the axioms where $P$ is a predicate is:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- You can change $P(x)$ to $x \in K$ to get the same definition we used earlier. Notice that $\forall P$ is a quantifier over all predicates, whereas $\forall n$ is a quantifier over all numbers.
- So yes, this can be understood as having bound variables which are first-order sentences themselves.
- ### Relation to second-order arithmetic
- The axiom of induction makes the formulation close to second-order arithmetic since second-order arithmetic uses:
- * The axiom of induction
- * The axiom of comprehension
- Thus we only need one more axiom to reach it. I won't go into much more detail, but in essence second-order arithmetic lets us define reals & rationals making is significantly stronger than PA.
- ### Peano Axioms as a first-order theory
- The axioms I presented earlier include a second-order axiom (the axiom of induction), as I discussed earlier. We can weaken it into a first-order theory by using an axiom schema.
- An axiom schema is simply an infinite list of axioms. So in this case, we can have a weaker version of:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- Where instead we say:
- 1. Generate a first-order formula $P$ (which we haven't generated yet)
- 2. Add the rule:
- $$P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n))$$
- This in essence makes the list of possible $P$ countable (whereas it was uncountable before).
It turns out this limits the types of sets in PA significantly.
- Yes, your right the axioms are (usually) written in first-order logic (FOL).
- However, we can "cheat" by using natural language to describe our axioms (which is done in the Wikipedia article).
- After all at some point some axioms will need to be defined in natural language.
- (e.g.: If Peano Axioms are defined in FOL, then what is FOL defined with?)
- Therefore to make them "primitive notions", we simply cheat by defining them in natural language.
- ### What are the Peano Axioms?
- The axioms of Peano Axioms (PA) are:
- * a) 0 is a natural number
- * b) For all natural numbers $n$, $S(n)$ is a natural number
- * c) For all natural numbers $n$ & $m$, if $S(n) = S(m)$, then $n = m$
- * d) For all natural numbers $n$, $S(n) = 0$ is false
- * e) Given a set $K$ which contains $0$,
- If whenever a natural numbers $n$ is in $K$ also means $S(n)$ is in $K$,
- Then $K$ contains all natural numbers.
- So the first 2 axioms are pretty intuitive, as they're required to create any structure with multiple elements:
- * a) We have the natural number: $0$
- *"We need a starting point"*
- * b) We now have natural numbers: $0, S(0), S(S(0)), ...$
- *"We can take steps from the starting point"*
- Now at this point, the natural numbers *could* be several sets. The following are alternative systems that have yet to be disqualified, meaning our axioms don't describe $\mathbb{N}$ in a satisfactory way:
- 1. **Preorder-like structure:**
- $\{ 0, a, S(0) \}$ where $S(0) = S(a)$ and $S(S(0)) = 0$
- 2. **Cyclic group of 3 elements:**
- $\{ 0, S(0), S(S(0)) \}$ and $S(S(S(0))) = 0$ or $\{ 0, 1, 2 \}$ are the only numbers and $2 + 1 = 0$
- 3. **Two zeros:**
- $\{ 0, a, S(0), S(a), S(S(0)), \dots \}$
- Graphically, we can visualize these in the following way:
- 
- * c) This successfully rules out (1) since $S(0) = S(a)$, but $a \neq 0$.
- We can interpret (c) as a type of linearization axiom where:
- *"There is only one path to get to a number by successive steps"*
- * d) This successfully rules out (2) since $S(S(0)) = 0$ contradicting the axiom.
- We can interpret (d) as a no-loops axiom where:
- *"There is no number whose next number is zero"*
- **(Notice this also rules out negative numbers, so it's also a no-negatives axiom)**
- * e) This axiom intuitively means: all natural numbers can be obtained by applying $S$ to $0$.
- This fails for (3), since $a$ cannot be obtained by applying $S$ to $0$. One way to put it is:
- *"All natural numbers are obtained from 0"*
- Now, one might think *are these axioms sufficient? Do we know if these actually are the natural numbers we think of intuitively?* The answer to both is *"we don't know"*. They seem to be sufficient for proving standard results in number theory, however whether they are *"actually the natural numbers"* is a philosophical question.
- ### Regarding the axioms of equality
- Notice that we used the notion of equality several times when defining the axioms. We used an operator $=$, and we forgot to define it.
- While we could argue that "equality is intuitive", formally it should be specified. This is what the equality axioms do.
- ### Regarding the axiom of induction
- The reason why this is a second-order statement, is actually hidden in our formulation. Notice however that we used the notion of a "set" in the definition. This is where the "second-order"-ness is coming in.
- We are saying something about "all sets", meaning we are using a quantifier over the "sets". This is what is second-order about it.
- Another formulation of the axioms where $P$ is a predicate is:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- You can change $P(x)$ to $x \in K$ to get the same definition we used earlier. Notice that $\forall P$ is a quantifier over all predicates, whereas $\forall n$ is a quantifier over all numbers.
- So yes, this can be understood as having bound variables which are first-order sentences themselves.
- ### Relation to second-order arithmetic
- The axiom of induction makes the formulation close to second-order arithmetic since second-order arithmetic uses:
- * The axiom of induction
- * The axiom of comprehension
- Thus we only need one more axiom to reach it. I won't go into much more detail, but in essence second-order arithmetic lets us define reals & rationals making is significantly stronger than PA.
- ### Peano Axioms as a first-order theory
- The axioms I presented earlier include a second-order axiom (the axiom of induction), as I discussed earlier. We can weaken it into a first-order theory by using an axiom schema.
- An axiom schema is simply an infinite list of axioms. So in this case, we can have a weaker version of:
- $$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
- Where instead we say:
- 1. Generate a first-order formula $P$ (which we haven't generated yet)
- 2. Add the rule:
- $$P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n))$$
- This in essence makes the list of possible $P$ countable (whereas it was uncountable before).
- It turns out this limits the types of sets in PA significantly.
- Therefore the PA we defined, stronger than this theory, but weaker than second-order arithmetic.
#1: Initial revision
Yes, your right the axioms are (usually) written in first-order logic (FOL).
However, we can "cheat" by using natural language to describe our axioms (which is done in the Wikipedia article).
After all at some point some axioms will need to be defined in natural language.
(e.g.: If Peano Axioms are defined in FOL, then what is FOL defined with?)
Therefore to make them "primitive notions", we simply cheat by defining them in natural language.
### What are the Peano Axioms?
The axioms of Peano Axioms (PA) are:
* a) 0 is a natural number
* b) For all natural numbers $n$, $S(n)$ is a natural number
* c) For all natural numbers $n$ & $m$, if $S(n) = S(m)$, then $n = m$
* d) For all natural numbers $n$, $S(n) = 0$ is false
* e) Given a set $K$ which contains $0$,
If whenever a natural numbers $n$ is in $K$ also means $S(n)$ is in $K$,
Then $K$ contains all natural numbers.
So the first 2 axioms are pretty intuitive, as they're required to create any structure with multiple elements:
* a) We have the natural number: $0$
*"We need a starting point"*
* b) We now have natural numbers: $0, S(0), S(S(0)), ...$
*"We can take steps from the starting point"*
Now at this point, the natural numbers *could* be several sets. The following are alternative systems that have yet to be disqualified, meaning our axioms don't describe $\mathbb{N}$ in a satisfactory way:
1. **Preorder-like structure:**
$\{ 0, a, S(0) \}$ where $S(0) = S(a)$ and $S(S(0)) = 0$
2. **Cyclic group of 3 elements:**
$\{ 0, S(0), S(S(0)) \}$ and $S(S(S(0))) = 0$ or $\{ 0, 1, 2 \}$ are the only numbers and $2 + 1 = 0$
3. **Two zeros:**
$\{ 0, a, S(0), S(a), S(S(0)), \dots \}$
Graphically, we can visualize these in the following way:

* c) This successfully rules out (1) since $S(0) = S(a)$, but $a \neq 0$.
We can interpret (c) as a type of linearization axiom where:
*"There is only one path to get to a number by successive steps"*
* d) This successfully rules out (2) since $S(S(0)) = 0$ contradicting the axiom.
We can interpret (d) as a no-loops axiom where:
*"There is no number whose next number is zero"*
**(Notice this also rules out negative numbers, so it's also a no-negatives axiom)**
* e) This axiom intuitively means: all natural numbers can be obtained by applying $S$ to $0$.
This fails for (3), since $a$ cannot be obtained by applying $S$ to $0$. One way to put it is:
*"All natural numbers are obtained from 0"*
Now, one might think *are these axioms sufficient? Do we know if these actually are the natural numbers we think of intuitively?* The answer to both is *"we don't know"*. They seem to be sufficient for proving standard results in number theory, however whether they are *"actually the natural numbers"* is a philosophical question.
### Regarding the axioms of equality
Notice that we used the notion of equality several times when defining the axioms. We used an operator $=$, and we forgot to define it.
While we could argue that "equality is intuitive", formally it should be specified. This is what the equality axioms do.
### Regarding the axiom of induction
The reason why this is a second-order statement, is actually hidden in our formulation. Notice however that we used the notion of a "set" in the definition. This is where the "second-order"-ness is coming in.
We are saying something about "all sets", meaning we are using a quantifier over the "sets". This is what is second-order about it.
Another formulation of the axioms where $P$ is a predicate is:
$$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
You can change $P(x)$ to $x \in K$ to get the same definition we used earlier. Notice that $\forall P$ is a quantifier over all predicates, whereas $\forall n$ is a quantifier over all numbers.
So yes, this can be understood as having bound variables which are first-order sentences themselves.
### Relation to second-order arithmetic
The axiom of induction makes the formulation close to second-order arithmetic since second-order arithmetic uses:
* The axiom of induction
* The axiom of comprehension
Thus we only need one more axiom to reach it. I won't go into much more detail, but in essence second-order arithmetic lets us define reals & rationals making is significantly stronger than PA.
### Peano Axioms as a first-order theory
The axioms I presented earlier include a second-order axiom (the axiom of induction), as I discussed earlier. We can weaken it into a first-order theory by using an axiom schema.
An axiom schema is simply an infinite list of axioms. So in this case, we can have a weaker version of:
$$\forall P( P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n)) )$$
Where instead we say:
1. Generate a first-order formula $P$ (which we haven't generated yet)
2. Add the rule:
$$P(0) \land \forall n ( P(n) \to P(n+1) ) \to \forall n (P(n))$$
This in essence makes the list of possible $P$ countable (whereas it was uncountable before).
It turns out this limits the types of sets in PA significantly.


















