Post History
#2: Post edited
by
Peter Taylor
·
2024-02-12T19:19:15Z (3 months ago)
Reduced the question metainformation to that which is relevant to this site
I am reposting my question from Proof Assistants Stack Exchange because due to being suspended I am unable to thank the person who posted an extraordinarily high quality answer - and award the 150 point bounty I had open on the question.I would very much appreciate if anyone seeing this could post the link to this Math Codidact post as a comment on that Stack Exchange post (the answer) so that the person who wrote the answer can see that I deeply appreciated their response. Thank you.https://proofassistants.stackexchange.com/questions/2707/a-program-which-could-derive-theorems-given-formation-rules-in-any-modal-logic——————- There are multiple modal logics which have different formation rules:
- 
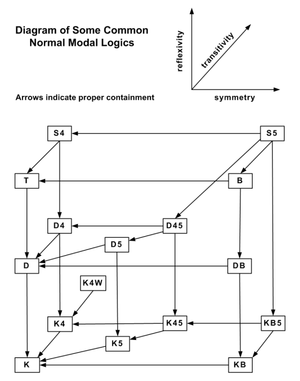
- Suppose someone asked the intuitive question, "If phi were a theorem in a modal logic M, what general, related conclusions might be drawn from that being so?" (See What is the modality of a statement that follows from a necessary statement? )
- I am picturing a program which can generate all theorems of a logic L which include a specific formation rule R (for example, the rule □P ⊢ P). There are two criteria I would have it fulfill: a) there must be a bound to how many theorems it should generate; and if necessary, b) an algorithm which "recognizes" interesting vs. non-interesting theorems.
- For a), I wonder if there are choices as how to one can define the bound. It could be the number of times of application of a formation rule (does this have a name? The "order" of a theorem?), or maybe there are other, better ways.
- For b), I anticipate this is because, since we are seeking interesting conclusions, we want a way to filter out a large amount of seemingly boring or trivial theorems.
- (Also, in case brute-force generation of all theorems is too combinatorially explosive, I am interested in algorithms which make more efficient choices in what theorems to generate.)
- Lastly, I would have such a program run over all modal logics L featuring formation rule R, so as to see what the implications of such a rule are across various logics, to compare them.
Can anyone please present a blueprint of such a program, in a programming language (of their choice)? I want a clear conceptual grasp of such a program more than implementable code, which I can write myself once I see the pitfalls, best practices and common design patterns and so on.
- There are multiple modal logics which have different formation rules:
- 
- Suppose someone asked the intuitive question, "If phi were a theorem in a modal logic M, what general, related conclusions might be drawn from that being so?" (See What is the modality of a statement that follows from a necessary statement? )
- I am picturing a program which can generate all theorems of a logic L which include a specific formation rule R (for example, the rule □P ⊢ P). There are two criteria I would have it fulfill: a) there must be a bound to how many theorems it should generate; and if necessary, b) an algorithm which "recognizes" interesting vs. non-interesting theorems.
- For a), I wonder if there are choices as how to one can define the bound. It could be the number of times of application of a formation rule (does this have a name? The "order" of a theorem?), or maybe there are other, better ways.
- For b), I anticipate this is because, since we are seeking interesting conclusions, we want a way to filter out a large amount of seemingly boring or trivial theorems.
- (Also, in case brute-force generation of all theorems is too combinatorially explosive, I am interested in algorithms which make more efficient choices in what theorems to generate.)
- Lastly, I would have such a program run over all modal logics L featuring formation rule R, so as to see what the implications of such a rule are across various logics, to compare them.
- Can anyone please present a blueprint of such a program, in a programming language (of their choice)? I want a clear conceptual grasp of such a program more than implementable code, which I can write myself once I see the pitfalls, best practices and common design patterns and so on.
- ---
- NB I originally asked this question [elsewhere](https://proofassistants.stackexchange.com/questions/2707/a-program-which-could-derive-theorems-given-formation-rules-in-any-modal-logic) and have copied across a very good CC-SA answer.
#1: Initial revision
by
Julius H.
·
2024-02-10T19:46:01Z (3 months ago)
A program which could derive theorems given formation rules in any modal logic?
I am reposting my question from Proof Assistants Stack Exchange because due to being suspended I am unable to thank the person who posted an extraordinarily high quality answer - and award the 150 point bounty I had open on the question. I would very much appreciate if anyone seeing this could post the link to this Math Codidact post as a comment on that Stack Exchange post (the answer) so that the person who wrote the answer can see that I deeply appreciated their response. Thank you. https://proofassistants.stackexchange.com/questions/2707/a-program-which-could-derive-theorems-given-formation-rules-in-any-modal-logic —————— There are multiple modal logics which have different formation rules:  Suppose someone asked the intuitive question, "If phi were a theorem in a modal logic M, what general, related conclusions might be drawn from that being so?" (See What is the modality of a statement that follows from a necessary statement? ) I am picturing a program which can generate all theorems of a logic L which include a specific formation rule R (for example, the rule □P ⊢ P). There are two criteria I would have it fulfill: a) there must be a bound to how many theorems it should generate; and if necessary, b) an algorithm which "recognizes" interesting vs. non-interesting theorems. For a), I wonder if there are choices as how to one can define the bound. It could be the number of times of application of a formation rule (does this have a name? The "order" of a theorem?), or maybe there are other, better ways. For b), I anticipate this is because, since we are seeking interesting conclusions, we want a way to filter out a large amount of seemingly boring or trivial theorems. (Also, in case brute-force generation of all theorems is too combinatorially explosive, I am interested in algorithms which make more efficient choices in what theorems to generate.) Lastly, I would have such a program run over all modal logics L featuring formation rule R, so as to see what the implications of such a rule are across various logics, to compare them. Can anyone please present a blueprint of such a program, in a programming language (of their choice)? I want a clear conceptual grasp of such a program more than implementable code, which I can write myself once I see the pitfalls, best practices and common design patterns and so on.