Post History
#3: Post edited
- Since, $\displaystyle \lim_{x\to 0}\frac{\sin x}{x}=1$, the singularity of the integral is not at $x=0$. On the other hand, one can rewrite the integral as
- $
- \int_{0}^\infty\frac{1}{x}\cdot |\sin(x)|\ dx\.
- $
- It suffices to analyze the sum
- $$
- \int_0^\pi\frac{\sin(x)}{x}\ dx+\int_{\pi}^{N\pi}\frac{1}{x}\cdot |\sin(x)|\ dx\.
- $$
- and show that it goes to $\infty$ as $N\to\infty$. Why integrate up to $N\pi$ instead of $N$? Well, partly due to technical convenience: the function $|\sin(x)|$ has the period of $\pi$. The graph of the integrand suggests that we may estimate the integral over each period and then add them together.
- As mentioned earlier, one can write the first integral as one for the continuous function. So we focus on the second one.
- On the interval $[\pi,2\pi]$, one has
- $$
- \int_\pi^{2\pi}\frac1x|\sin(x)|\ dx\ge \frac1{2\pi}\int_\pi^{2\pi}|\sin(x)|\ dx= \frac{1}{2\pi}\cdot 2
- $$
- where we use the simple fact that $\int_a^b f(x)\ dx\ge \int_a^b g(x)\ dx$ if $f(x)\ge g(x)$ on $[a,b]$.
- We work with the *lower bounds* because in order to show something diverges, big lower bounds would help.
- Similarly, on the interval, $[2\pi,3\pi]$, we have
- $$
- \int_{2\pi}^{3\pi}\frac1x|\sin(x)|\ dx\ge \frac1{3\pi}\int_{2\pi}^{3\pi}|\sin(x)|\ dx= \frac{1}{3\pi}\cdot 2
- $$
- and in general,
- $$
- \int_{(n-1)\pi}^{n\pi}\frac1x|\sin(x)|\ dx\ge \frac1{n\pi}\int_{(n-1)\pi}^{n\pi}|\sin(x)|\ dx = \frac{1}{n\pi}\cdot 2
- $$
- By adding the estimates together and using the fact that the harmonic series diverges, we have the desired proof.
- Since, $\displaystyle \lim_{x\to 0}\frac{\sin x}{x}=1$, the singularity of the integral is not at $x=0$. On the other hand, one can rewrite the integral as
- $
- \int_{0}^\infty\frac{1}{x}\cdot |\sin(x)|\ dx\.
- $
- It suffices to analyze the sum
- $$
- \int_0^\pi\frac{\sin(x)}{x}\ dx+\int_{\pi}^{N\pi}\frac{1}{x}\cdot |\sin(x)|\ dx\.
- $$
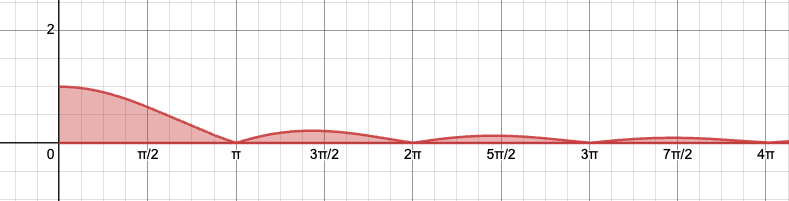
- and show that it goes to $\infty$ as $N\to\infty$. Why integrate up to $N\pi$ instead of $N$? Well, partly due to technical convenience: the function $|\sin(x)|$ has the period of $\pi$. The graph of the integrand suggests that we may estimate the integral over each period and then add them together.
- 
- As mentioned earlier, one can write the first integral as one for the continuous function. So we focus on the second one.
- On the interval $[\pi,2\pi]$, one has
- $$
- \int_\pi^{2\pi}\frac1x|\sin(x)|\ dx\ge \frac1{2\pi}\int_\pi^{2\pi}|\sin(x)|\ dx= \frac{1}{2\pi}\cdot 2
- $$
- where we use the simple fact that $\int_a^b f(x)\ dx\ge \int_a^b g(x)\ dx$ if $f(x)\ge g(x)$ on $[a,b]$.
- We work with the *lower bounds* because in order to show something diverges, big lower bounds would help.
- Similarly, on the interval, $[2\pi,3\pi]$, we have
- $$
- \int_{2\pi}^{3\pi}\frac1x|\sin(x)|\ dx\ge \frac1{3\pi}\int_{2\pi}^{3\pi}|\sin(x)|\ dx= \frac{1}{3\pi}\cdot 2
- $$
- and in general,
- $$
- \int_{(n-1)\pi}^{n\pi}\frac1x|\sin(x)|\ dx\ge \frac1{n\pi}\int_{(n-1)\pi}^{n\pi}|\sin(x)|\ dx = \frac{1}{n\pi}\cdot 2
- $$
- By adding the estimates together and using the fact that the harmonic series diverges, we have the desired proof.
#2: Post edited
- Since, $\displaystyle \lim_{x\to 0}\frac{\sin x}{x}=1$, the singularity of the integral is not at $x=0$. On the other hand, one can rewrite the integral as
- $
- \int_{0}^\infty\frac{1}{x}\cdot |\sin(x)|\ dx\.
- $
- It suffices to analyze the sum
- $$
- \int_0^\pi\frac{\sin(x)}{x}\ dx+\int_{\pi}^{N\pi}\frac{1}{x}\cdot |\sin(x)|\ dx\.
- $$
- and show that it goes to $\infty$ as $N\to\infty$. Why integrate up to $N\pi$ instead of $N$? Well, partly due to technical convenience: the function $|\sin(x)|$ has the period of $\pi$. The graph of the integrand suggests that we may estimate the integral over each period and then add them together.
- As mentioned earlier, one can write the first integral as one for the continuous function. So we focus on the second one.
- On the interval $[\pi,2\pi]$, one has
- $$
- \int_\pi^{2\pi}\frac1x|\sin(x)|\ dx\ge \frac1{2\pi}\int_\pi^{2\pi}|\sin(x)|\ dx= \frac{1}{2\pi}\cdot 2
- $$
- where we use the simple fact that $\int_a^b f(x)\ dx\ge \int_a^b g(x)\ dx$ if $f(x)\ge g(x)$ on $[a,b]$.
- We work with the *lower bounds* because in order to show something diverges, big lower bounds would help.
- Similarly, on the interval, $[2\pi,3\pi]$, we have
- $$
- \int_{2\pi}^{3\pi}\frac1x|\sin(x)|\ dx\ge \frac1{3\pi}\int_{2\pi}^{3\pi}|\sin(x)|\ dx= \frac{1}{3\pi}\cdot 2
- $$
- and in general,
- $$
- \int_{(n-1)\pi}^{n\pi}\frac1x|\sin(x)|\ dx\ge \frac1{n\pi}\int_{(n-1)\pi}^{n\pi}|\sin(x)|\ dx = \frac{1}{n\pi}\cdot 2
- $$
- By adding the estimates together and using the fact that the harmonic series diverges, we have the desired proof.
- Since, $\displaystyle \lim_{x\to 0}\frac{\sin x}{x}=1$, the singularity of the integral is not at $x=0$. On the other hand, one can rewrite the integral as
- $
- \int_{0}^\infty\frac{1}{x}\cdot |\sin(x)|\ dx\.
- $
- It suffices to analyze the sum
- $$
- \int_0^\pi\frac{\sin(x)}{x}\ dx+\int_{\pi}^{N\pi}\frac{1}{x}\cdot |\sin(x)|\ dx\.
- $$
- and show that it goes to $\infty$ as $N\to\infty$. Why integrate up to $N\pi$ instead of $N$? Well, partly due to technical convenience: the function $|\sin(x)|$ has the period of $\pi$. The graph of the integrand suggests that we may estimate the integral over each period and then add them together.
- 
- As mentioned earlier, one can write the first integral as one for the continuous function. So we focus on the second one.
- On the interval $[\pi,2\pi]$, one has
- $$
- \int_\pi^{2\pi}\frac1x|\sin(x)|\ dx\ge \frac1{2\pi}\int_\pi^{2\pi}|\sin(x)|\ dx= \frac{1}{2\pi}\cdot 2
- $$
- where we use the simple fact that $\int_a^b f(x)\ dx\ge \int_a^b g(x)\ dx$ if $f(x)\ge g(x)$ on $[a,b]$.
- We work with the *lower bounds* because in order to show something diverges, big lower bounds would help.
- Similarly, on the interval, $[2\pi,3\pi]$, we have
- $$
- \int_{2\pi}^{3\pi}\frac1x|\sin(x)|\ dx\ge \frac1{3\pi}\int_{2\pi}^{3\pi}|\sin(x)|\ dx= \frac{1}{3\pi}\cdot 2
- $$
- and in general,
- $$
- \int_{(n-1)\pi}^{n\pi}\frac1x|\sin(x)|\ dx\ge \frac1{n\pi}\int_{(n-1)\pi}^{n\pi}|\sin(x)|\ dx = \frac{1}{n\pi}\cdot 2
- $$
- By adding the estimates together and using the fact that the harmonic series diverges, we have the desired proof.
#1: Initial revision
Since, $\displaystyle \lim_{x\to 0}\frac{\sin x}{x}=1$, the singularity of the integral is not at $x=0$. On the other hand, one can rewrite the integral as
$
\int_{0}^\infty\frac{1}{x}\cdot |\sin(x)|\ dx\.
$
It suffices to analyze the sum
$$
\int_0^\pi\frac{\sin(x)}{x}\ dx+\int_{\pi}^{N\pi}\frac{1}{x}\cdot |\sin(x)|\ dx\.
$$
and show that it goes to $\infty$ as $N\to\infty$. Why integrate up to $N\pi$ instead of $N$? Well, partly due to technical convenience: the function $|\sin(x)|$ has the period of $\pi$. The graph of the integrand suggests that we may estimate the integral over each period and then add them together.
As mentioned earlier, one can write the first integral as one for the continuous function. So we focus on the second one.
On the interval $[\pi,2\pi]$, one has
$$
\int_\pi^{2\pi}\frac1x|\sin(x)|\ dx\ge \frac1{2\pi}\int_\pi^{2\pi}|\sin(x)|\ dx= \frac{1}{2\pi}\cdot 2
$$
where we use the simple fact that $\int_a^b f(x)\ dx\ge \int_a^b g(x)\ dx$ if $f(x)\ge g(x)$ on $[a,b]$.
We work with the *lower bounds* because in order to show something diverges, big lower bounds would help.
Similarly, on the interval, $[2\pi,3\pi]$, we have
$$
\int_{2\pi}^{3\pi}\frac1x|\sin(x)|\ dx\ge \frac1{3\pi}\int_{2\pi}^{3\pi}|\sin(x)|\ dx= \frac{1}{3\pi}\cdot 2
$$
and in general,
$$
\int_{(n-1)\pi}^{n\pi}\frac1x|\sin(x)|\ dx\ge \frac1{n\pi}\int_{(n-1)\pi}^{n\pi}|\sin(x)|\ dx = \frac{1}{n\pi}\cdot 2
$$
By adding the estimates together and using the fact that the harmonic series diverges, we have the desired proof.


















