Post History
#2: Post edited
- This is a [synthetic geometry](https://en.wikipedia.org/wiki/Synthetic_geometry) approach to the problem. It turned out more involved than I expected, and yet I haven’t found anything that could be omitted! I don’t say there *isn’t* a shorter way to do it, though, probably using some theorems that I haven’t thought of. (Maybe circle inversion? Seems like someone always pulls out circle inversion for knotty geometry problems.)
- I also have a nice, direct solution using trigonometry. I haven’t yet solved it using vectors as you asked, because in the middle of my vector approach I keep reaching for *trigonometric* relationships, like the sine rule.
- ---
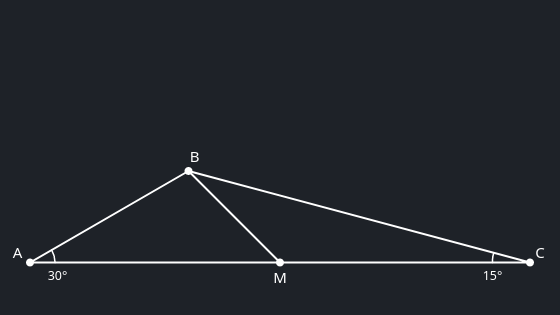
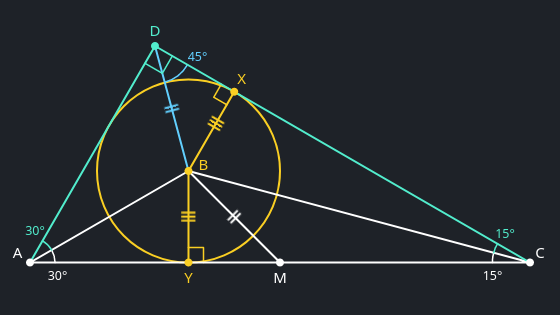
- So here’s the situation as it’s given.
- 
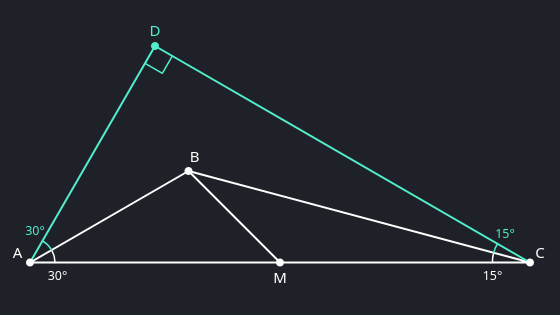
- To begin, double the known angles: reflect $AC$ across $AB$ to double the 30° angle, and reflect $AC$ across $BC$ to double the 15° angle. Call the intersection of these reflected lines $D$. Since our newly doubled angles are $\angle CAD = 60°$ and $\angle ACD = 30°$, the angle sum of $\triangle ACD$ tells us that $\angle ADC = 90°$.
- 
In a right triangle like $\triangle ADC$, the circumcentre is the midpoint of the hypotenuse—$M$ in this case. So $|AM| = |DM|$, and $\triangle ADM$ at least isosceles. But since $\angle MAD = 60°$, this triangle is in fact equilateral, with $|AM| = |DM| = |AD|$.- 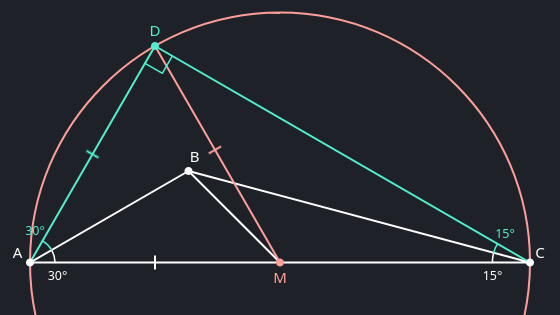
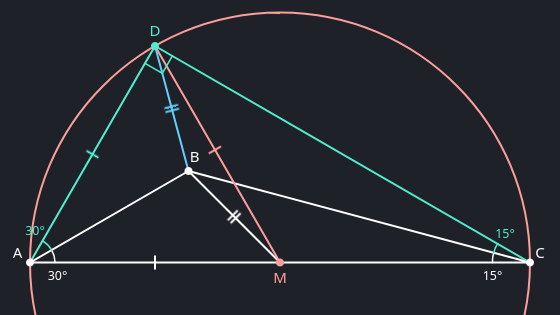
- Now, since equilateral triangles are so charmingly symmetrical, the angle bisector $AB$ is also the perpendicular bisector of the opposite side $DM$ (or would be, if we extended it). That makes any point on it, $B$ included, equidistant from $D$ and $M$. So $\triangle BDM$ is isosceles.
- 
- Speaking of angle bisectors, the angle bisectors of any triangle concur at its incentre. As the intersection of $AB$ (bisecting $\angle CAD$) and $BC$ (bisecting $\angle ACD$), $B$ is the incentre of $\triangle ACD$. As $BD$ connects this incentre to the remaining vertex, it is also an angle bisector, bisecting $\angle ADC$. As that’s a right angle, $\angle BDC = 45°$.
- Let $X$ and $Y$ be the tangent points of the incircle on sides $CD$ and $AC$, respectively. As radii and tangents are perpendicular, $BX \perp CD$ and $BY \perp AC$.
- 
- By the RHS criterion, $\triangle BMY \cong \triangle BDX$, so $\angle BMY = 45°$ as well.
- 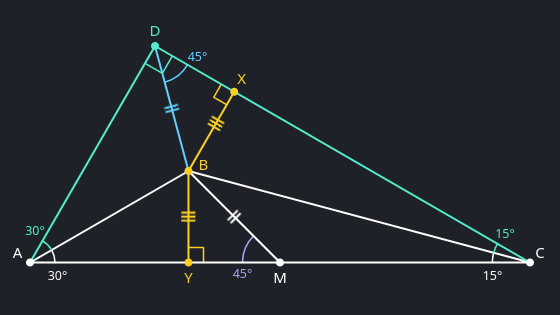
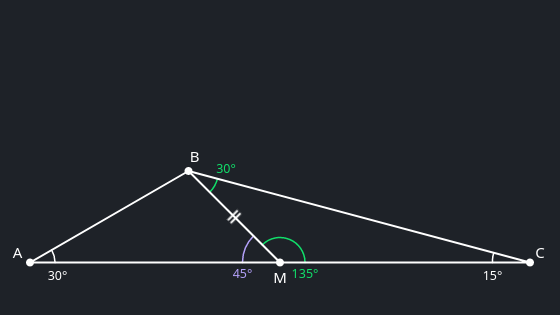
- Hence, its complementary angle $\angle BMC = 135°$, and by the angle sum of $\triangle BCM$, $\angle CBM = 30°$. ∎
- 
- This is a [synthetic geometry](https://en.wikipedia.org/wiki/Synthetic_geometry) approach to the problem. It turned out more involved than I expected, and yet I haven’t found anything that could be omitted! I don’t say there *isn’t* a shorter way to do it, though, probably using some theorems that I haven’t thought of. (Maybe circle inversion? Seems like someone always pulls out circle inversion for knotty geometry problems.)
- I also have a nice, direct solution using trigonometry. I haven’t yet solved it using vectors as you asked, because in the middle of my vector approach I keep reaching for *trigonometric* relationships, like the sine rule.
- ---
- So here’s the situation as it’s given.
- 
- To begin, double the known angles: reflect $AC$ across $AB$ to double the 30° angle, and reflect $AC$ across $BC$ to double the 15° angle. Call the intersection of these reflected lines $D$. Since our newly doubled angles are $\angle CAD = 60°$ and $\angle ACD = 30°$, the angle sum of $\triangle ACD$ tells us that $\angle ADC = 90°$.
- 
- In a right triangle like $\triangle ADC$, the circumcentre is the midpoint of the hypotenuse—$M$ in this case. So $|AM| = |DM|$, and $\triangle ADM$ is at least isosceles. But since $\angle MAD = 60°$, this triangle is in fact equilateral, with $|AM| = |DM| = |AD|$.
- 
- Now, since equilateral triangles are so charmingly symmetrical, the angle bisector $AB$ is also the perpendicular bisector of the opposite side $DM$ (or would be, if we extended it). That makes any point on it, $B$ included, equidistant from $D$ and $M$. So $\triangle BDM$ is isosceles.
- 
- Speaking of angle bisectors, the angle bisectors of any triangle concur at its incentre. As the intersection of $AB$ (bisecting $\angle CAD$) and $BC$ (bisecting $\angle ACD$), $B$ is the incentre of $\triangle ACD$. As $BD$ connects this incentre to the remaining vertex, it is also an angle bisector, bisecting $\angle ADC$. As that’s a right angle, $\angle BDC = 45°$.
- Let $X$ and $Y$ be the tangent points of the incircle on sides $CD$ and $AC$, respectively. As radii and tangents are perpendicular, $BX \perp CD$ and $BY \perp AC$.
- 
- By the RHS criterion, $\triangle BMY \cong \triangle BDX$, so $\angle BMY = 45°$ as well.
- 
- Hence, its complementary angle $\angle BMC = 135°$, and by the angle sum of $\triangle BCM$, $\angle CBM = 30°$. ∎
- 
#1: Initial revision
This is a [synthetic geometry](https://en.wikipedia.org/wiki/Synthetic_geometry) approach to the problem. It turned out more involved than I expected, and yet I haven’t found anything that could be omitted! I don’t say there *isn’t* a shorter way to do it, though, probably using some theorems that I haven’t thought of. (Maybe circle inversion? Seems like someone always pulls out circle inversion for knotty geometry problems.) I also have a nice, direct solution using trigonometry. I haven’t yet solved it using vectors as you asked, because in the middle of my vector approach I keep reaching for *trigonometric* relationships, like the sine rule. --- So here’s the situation as it’s given.  To begin, double the known angles: reflect $AC$ across $AB$ to double the 30° angle, and reflect $AC$ across $BC$ to double the 15° angle. Call the intersection of these reflected lines $D$. Since our newly doubled angles are $\angle CAD = 60°$ and $\angle ACD = 30°$, the angle sum of $\triangle ACD$ tells us that $\angle ADC = 90°$.  In a right triangle like $\triangle ADC$, the circumcentre is the midpoint of the hypotenuse—$M$ in this case. So $|AM| = |DM|$, and $\triangle ADM$ at least isosceles. But since $\angle MAD = 60°$, this triangle is in fact equilateral, with $|AM| = |DM| = |AD|$.  Now, since equilateral triangles are so charmingly symmetrical, the angle bisector $AB$ is also the perpendicular bisector of the opposite side $DM$ (or would be, if we extended it). That makes any point on it, $B$ included, equidistant from $D$ and $M$. So $\triangle BDM$ is isosceles.  Speaking of angle bisectors, the angle bisectors of any triangle concur at its incentre. As the intersection of $AB$ (bisecting $\angle CAD$) and $BC$ (bisecting $\angle ACD$), $B$ is the incentre of $\triangle ACD$. As $BD$ connects this incentre to the remaining vertex, it is also an angle bisector, bisecting $\angle ADC$. As that’s a right angle, $\angle BDC = 45°$. Let $X$ and $Y$ be the tangent points of the incircle on sides $CD$ and $AC$, respectively. As radii and tangents are perpendicular, $BX \perp CD$ and $BY \perp AC$.  By the RHS criterion, $\triangle BMY \cong \triangle BDX$, so $\angle BMY = 45°$ as well.  Hence, its complementary angle $\angle BMC = 135°$, and by the angle sum of $\triangle BCM$, $\angle CBM = 30°$. ∎ 


















