Post History
#4: Post edited
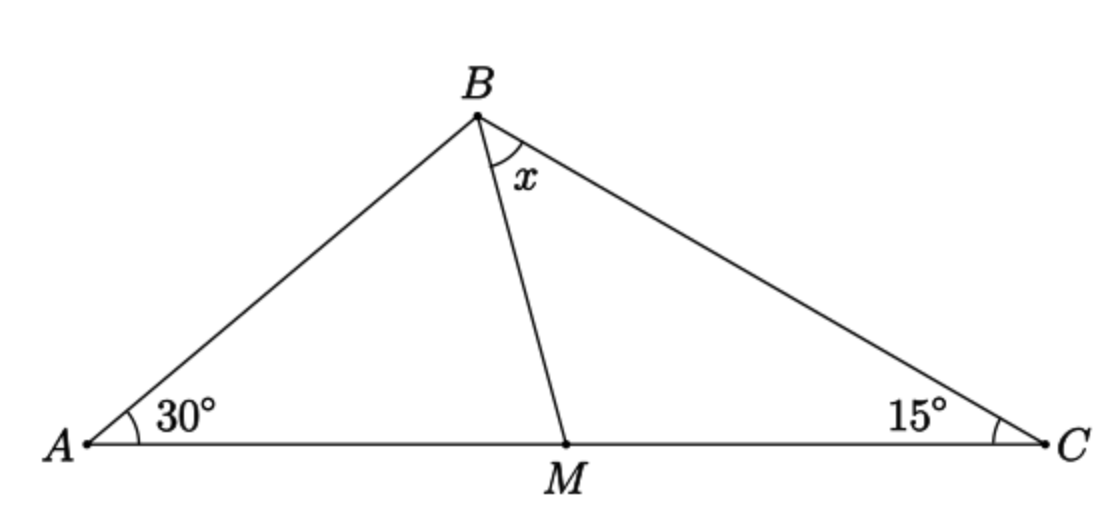
- > **Problem**: Suppose in $\triangle ABC$, $\angle BAC = 30^\circ$ and $\angle BCA = 15^\circ$. Suppose $BM$ is a [median](https://en.wikipedia.org/wiki/Median_(geometry)) of $\triangle ABC$. Show that $\angle MBC=\angle BAC$.
- > 
- $\def\vecl{\overrightarrow}$
- Remark: One may of course try to use congruent or similar triangles. I am wondering if one can solve the problem by using vectors in $\mathbf{R}^2$: for instance, can one somehow show by manipulating vectors that
- $$
\frac{\vecl{BM}\cdot\vecl{BC}}{\|\vecl{BM}\|\|\vecl{BC}\|}=\cos(\frac{\pi}{3})\ ?- $$
- > **Problem**: Suppose in $\triangle ABC$, $\angle BAC = 30^\circ$ and $\angle BCA = 15^\circ$. Suppose $BM$ is a [median](https://en.wikipedia.org/wiki/Median_(geometry)) of $\triangle ABC$. Show that $\angle MBC=\angle BAC$.
- > 
- $\def\vecl{\overrightarrow}$
- Remark: One may of course try to use congruent or similar triangles. I am wondering if one can solve the problem by using vectors in $\mathbf{R}^2$: for instance, can one somehow show by manipulating vectors that
- $$
- \frac{\vecl{BM}\cdot\vecl{BC}}{\|\vecl{BM}\|\|\vecl{BC}\|}=\cos(\frac{\pi}{6})\ ?
- $$
#3: Post edited
> **Problem**: Suppose in $\triangle ABC$, $\angle BAC = 30^\circ$ and $\angle BCA = 15^\circ$. Suppose $BM$ is a [median](https://en.wikipedia.org/wiki/Median_(geometry)) of $\triangle ABC$ Show that $\angle MBC=30^\circ$.> - $\def\vecl{\overrightarrow}$
- Remark: One may of course try to use congruent or similar triangles. I am wondering if one can solve the problem by using vectors in $\mathbf{R}^2$: for instance, can one somehow show by manipulating vectors that
- $$
- \frac{\vecl{BM}\cdot\vecl{BC}}{\|\vecl{BM}\|\|\vecl{BC}\|}=\cos(\frac{\pi}{3})\ ?
- $$
- > **Problem**: Suppose in $\triangle ABC$, $\angle BAC = 30^\circ$ and $\angle BCA = 15^\circ$. Suppose $BM$ is a [median](https://en.wikipedia.org/wiki/Median_(geometry)) of $\triangle ABC$. Show that $\angle MBC=\angle BAC$.
- > 
- $\def\vecl{\overrightarrow}$
- Remark: One may of course try to use congruent or similar triangles. I am wondering if one can solve the problem by using vectors in $\mathbf{R}^2$: for instance, can one somehow show by manipulating vectors that
- $$
- \frac{\vecl{BM}\cdot\vecl{BC}}{\|\vecl{BM}\|\|\vecl{BC}\|}=\cos(\frac{\pi}{3})\ ?
- $$
#1: Initial revision
Given two angles of a triangle, finding an angle formed by a median
> **Problem**: Suppose in $\triangle ABC$, $\angle BAC = 30^\circ$ and $\angle BCA = 15^\circ$. Suppose $BM$ is a [median](https://en.wikipedia.org/wiki/Median_(geometry)) of $\triangle ABC$ Show that $\angle MBC=30^\circ$.
> 
$\def\vecl{\overrightarrow}$
Remark: One may of course try to use congruent or similar triangles. I am wondering if one can solve the problem by using vectors in $\mathbf{R}^2$: for instance, can one somehow show by manipulating vectors that
$$
\frac{\vecl{BM}\cdot\vecl{BC}}{\|\vecl{BM}\|\|\vecl{BC}\|}=\cos(\frac{\pi}{3})\ ?
$$


















