Communities

Writing
Writing
Codidact Meta
Codidact Meta
The Great Outdoors
The Great Outdoors
Photography & Video
Photography & Video
Scientific Speculation
Scientific Speculation
Cooking
Cooking
Electrical Engineering
Electrical Engineering
Judaism
Judaism
Languages & Linguistics
Languages & Linguistics
Software Development
Software Development
Mathematics
Mathematics
Christianity
Christianity
Code Golf
Code Golf
Music
Music
Physics
Physics
Linux Systems
Linux Systems
Power Users
Power Users
Tabletop RPGs
Tabletop RPGs
Community Proposals
Community Proposals
tag:snake search within a tag
answers:0 unanswered questions
user:xxxx search by author id
score:0.5 posts with 0.5+ score
"snake oil" exact phrase
votes:4 posts with 4+ votes
created:<1w created < 1 week ago
post_type:xxxx type of post
Search help
Notifications
Mark all as read See all your notifications »
Users Search
Help Dashboard Sign In Sign Up
Q&A Meta
Q&A
Posts Tags Edits
Ask Question

Post History

66%
+2 −0
Q&A Is there a way to encode a unique arrangement of vertices of a graph with a unique short word?

posted 2y ago by celtschk‭  ·  edited 2y ago by celtschk‭

Answer
#5: Post edited by user avatar celtschk‭ · 2022-08-13T09:12:57Z (over 2 years ago)
I noticed that with my example in between, it wasn't cear where the example ended; so I moved the example to the end and wen't completely through the procedure with it
  • I'm going to assume your points are lying on an integer grid. I'm also assuming you always have a finite number of points.
  • Then one way to make words for your point clouds is to enumerate the grid points, for example by starting at the origin and going in a spiral. Then you can assign an unique finite bit-string to each configuration by starting at the origin, following the spiral and note a $0$ for any unoccupied grid point, and a $1$ for any occupied grid point, terminating as soon as you've covered all points (that is, all occupied grid points). Note that the last obtained digit that way is always a $1$.
  • Let's look at an example:
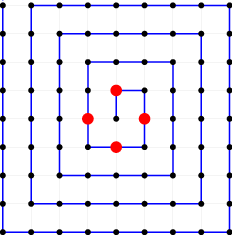
  • ![grid with points and spiral](https://math.codidact.com/uploads/dZqVvPRALnVkx3cWnxyXfynQ)
  • Here we see a graph with four points at the coordinates $(0,\pm 1)$, and $(\pm 1, 0)$. Starting at the origin (beginning of the spiral), we get the bit string $01010101$. Note that after the fourth $1$, we've covered all the dots, therefore we stop.
  • Now reverse that bit string. This ensures the first it is always $1$ (except for the empty cloud, which gets a single $0$), and therefore you can interpret the bit string as binary representation of a natural number, thus getting a bijection between point configurations and natural numbers.
  • Now all that remains is to map natural numbers to words. That's a pretty standard problem, and the best way to do so depends on the typical properties of your point arrangements. For example, if your points are generally always close to the origin, then you may just convert the number to base 26, and write it down using the 26 letters of the alphabet as digits. OTOH that may be a bad strategy if your points are frequently far from the origin.
  • I'm going to assume your points are lying on an integer grid. I'm also assuming you always have a finite number of points.
  • Then one way to make words for your point clouds is to enumerate the grid points, for example by starting at the origin and going in a spiral. Then you can assign an unique finite bit-string to each configuration by starting at the origin, following the spiral and note a $0$ for any unoccupied grid point, and a $1$ for any occupied grid point, terminating as soon as you've covered all points (that is, all occupied grid points). Note that the last obtained digit that way is always a $1$.
  • Now reverse that bit string. This ensures the first it is always $1$ (except for the empty cloud, which gets a single $0$), and therefore you can interpret the bit string as binary representation of a natural number, thus getting a bijection between point configurations and natural numbers.
  • Now all that remains is to map natural numbers to words. That's a pretty standard problem, and the best way to do so depends on the typical properties of your point arrangements. For example, if your points are generally always close to the origin, then you may just convert the number to base 26, and write it down using the 26 letters of the alphabet as digits. OTOH that may be a bad strategy if your points are frequently far from the origin.
  • Let's look at an example:
  • ![grid with points and spiral](https://math.codidact.com/uploads/dZqVvPRALnVkx3cWnxyXfynQ)
  • Here we see a graph with four points at the coordinates $(0,\pm 1)$, and $(\pm 1, 0)$. Starting at the origin (beginning of the spiral), we get the bit string $01010101$. Note that after the fourth $1$, we've covered all the dots, therefore we stop.
  • Reversing the bit string then gives $10101010$, which corresponds to the number $90$. Using the base-26 strategy with a=0, b=1, …, z=25, the resulting word is `dm`.
#4: Post edited by user avatar celtschk‭ · 2022-08-12T17:01:40Z (over 2 years ago)
fixed typo
  • I'm going to assume your points are lying on an integer grid. I'm also assuming you always have a finite number of points.
  • Then one way to make words for your point clouds is to enumerate the grid points, for example by starting at the origin and going in a spiral. Then you can assign an unique finite bit-string to each configuration by starting at the origin, following the spiral and note a $0$ for any unoccupied grid point, and a $1$ for any occupied grid point, terminating as soon as you've covered all points (that is, all occupied grid points). Note that the last obtained digit that way is always a $1$.
  • Let's look at an example:
  • ![grid with points and spiral](https://math.codidact.com/uploads/dZqVvPRALnVkx3cWnxyXfynQ)
  • Here we see a graph with four points at the coordinates $(0,\pm 1)$, and $(\pm 1, 0)$. Starring at the origin (beginning of the spiral), we get the bit string $01010101$. Note that after the fourth $1$, we've covered all the dots, therefore we stop.
  • Now reverse that bit string. This ensures the first it is always $1$ (except for the empty cloud, which gets a single $0$), and therefore you can interpret the bit string as binary representation of a natural number, thus getting a bijection between point configurations and natural numbers.
  • Now all that remains is to map natural numbers to words. That's a pretty standard problem, and the best way to do so depends on the typical properties of your point arrangements. For example, if your points are generally always close to the origin, then you may just convert the number to base 26, and write it down using the 26 letters of the alphabet as digits. OTOH that may be a bad strategy if your points are frequently far from the origin.
  • I'm going to assume your points are lying on an integer grid. I'm also assuming you always have a finite number of points.
  • Then one way to make words for your point clouds is to enumerate the grid points, for example by starting at the origin and going in a spiral. Then you can assign an unique finite bit-string to each configuration by starting at the origin, following the spiral and note a $0$ for any unoccupied grid point, and a $1$ for any occupied grid point, terminating as soon as you've covered all points (that is, all occupied grid points). Note that the last obtained digit that way is always a $1$.
  • Let's look at an example:
  • ![grid with points and spiral](https://math.codidact.com/uploads/dZqVvPRALnVkx3cWnxyXfynQ)
  • Here we see a graph with four points at the coordinates $(0,\pm 1)$, and $(\pm 1, 0)$. Starting at the origin (beginning of the spiral), we get the bit string $01010101$. Note that after the fourth $1$, we've covered all the dots, therefore we stop.
  • Now reverse that bit string. This ensures the first it is always $1$ (except for the empty cloud, which gets a single $0$), and therefore you can interpret the bit string as binary representation of a natural number, thus getting a bijection between point configurations and natural numbers.
  • Now all that remains is to map natural numbers to words. That's a pretty standard problem, and the best way to do so depends on the typical properties of your point arrangements. For example, if your points are generally always close to the origin, then you may just convert the number to base 26, and write it down using the 26 letters of the alphabet as digits. OTOH that may be a bad strategy if your points are frequently far from the origin.
#3: Post edited by user avatar celtschk‭ · 2022-08-12T16:57:42Z (over 2 years ago)
Added example with image for clarity
  • I'm going to assume your points are lying on an integer grid. I'm also assuming you always have a finite number of points.
  • Then one way to make words for your point clouds is to enumerate the grid points, for example by starting at the origin and going in a spiral. Then you can assign an unique finite bit-string to each configuration by starting at the origin, following the spiral and note a $0$ for any unoccupied grid point, and a $1$ for any occupied grid point, terminating as soon as you've covered all points (that is, all occupied grid points). Note that the last obtained digit that way is always a $1$.
  • Now reverse that bit string. This ensures the first it is always $1$ (except for the empty cloud, which gets a single $0$), and therefore you can interpret the bit string as binary representation of a natural number, thus getting a bijection between point configurations and natural numbers.
  • Now all that remains is to map natural numbers to words. That's a pretty standard problem, and the best way to do so depends on the typical properties of your point arrangements. For example, if your points are generally always close to the origin, then you may just convert the number to base 26, and write it down using the 26 letters of the alphabet as digits. OTOH that may be a bad strategy if your points are frequently far from the origin.
  • I'm going to assume your points are lying on an integer grid. I'm also assuming you always have a finite number of points.
  • Then one way to make words for your point clouds is to enumerate the grid points, for example by starting at the origin and going in a spiral. Then you can assign an unique finite bit-string to each configuration by starting at the origin, following the spiral and note a $0$ for any unoccupied grid point, and a $1$ for any occupied grid point, terminating as soon as you've covered all points (that is, all occupied grid points). Note that the last obtained digit that way is always a $1$.
  • Let's look at an example:
  • ![grid with points and spiral](https://math.codidact.com/uploads/dZqVvPRALnVkx3cWnxyXfynQ)
  • Here we see a graph with four points at the coordinates $(0,\pm 1)$, and $(\pm 1, 0)$. Starring at the origin (beginning of the spiral), we get the bit string $01010101$. Note that after the fourth $1$, we've covered all the dots, therefore we stop.
  • Now reverse that bit string. This ensures the first it is always $1$ (except for the empty cloud, which gets a single $0$), and therefore you can interpret the bit string as binary representation of a natural number, thus getting a bijection between point configurations and natural numbers.
  • Now all that remains is to map natural numbers to words. That's a pretty standard problem, and the best way to do so depends on the typical properties of your point arrangements. For example, if your points are generally always close to the origin, then you may just convert the number to base 26, and write it down using the 26 letters of the alphabet as digits. OTOH that may be a bad strategy if your points are frequently far from the origin.
#2: Post edited by user avatar celtschk‭ · 2022-08-12T07:20:39Z (over 2 years ago)
Noted special case
  • I'm going to assume your points are lying on an integer grid. I'm also assuming you always have a finite number of points.
  • Then one way to make words for your point clouds is to enumerate the grid points, for example by starting at the origin and going in a spiral. Then you can assign an unique finite bit-string to each configuration by starting at the origin, following the spiral and note a $0$ for any unoccupied grid point, and a $1$ for any occupied grid point, terminating as soon as you've covered all points (that is, all occupied grid points). Note that the last obtained digit that way is always a $1$.
  • Now reverse that bit string. This ensures the first it is always $1$, and therefore you can interpret the bit string as binary representation of a natural number, thus getting a bijection between point configurations and natural numbers.
  • Now all that remains is to map natural numbers to words. That's a pretty standard problem, and the best way to do so depends on the typical properties of your point arrangements. For example, if your points are generally always close to the origin, then you may just convert the number to base 26, and write it down using the 26 letters of the alphabet as digits. OTOH that may be a bad strategy if your points are frequently far from the origin.
  • I'm going to assume your points are lying on an integer grid. I'm also assuming you always have a finite number of points.
  • Then one way to make words for your point clouds is to enumerate the grid points, for example by starting at the origin and going in a spiral. Then you can assign an unique finite bit-string to each configuration by starting at the origin, following the spiral and note a $0$ for any unoccupied grid point, and a $1$ for any occupied grid point, terminating as soon as you've covered all points (that is, all occupied grid points). Note that the last obtained digit that way is always a $1$.
  • Now reverse that bit string. This ensures the first it is always $1$ (except for the empty cloud, which gets a single $0$), and therefore you can interpret the bit string as binary representation of a natural number, thus getting a bijection between point configurations and natural numbers.
  • Now all that remains is to map natural numbers to words. That's a pretty standard problem, and the best way to do so depends on the typical properties of your point arrangements. For example, if your points are generally always close to the origin, then you may just convert the number to base 26, and write it down using the 26 letters of the alphabet as digits. OTOH that may be a bad strategy if your points are frequently far from the origin.
#1: Initial revision by user avatar celtschk‭ · 2022-08-12T07:18:38Z (over 2 years ago) 
I'm going to assume your points are lying on an integer grid. I'm also assuming you always have a finite number of points.

Then one way to make words for your point clouds is to enumerate the grid points, for example by starting at the origin and going in a spiral. Then you can assign an unique finite bit-string to each configuration by starting at the origin, following the spiral and note a $0$ for any unoccupied grid point, and a $1$ for any occupied grid point, terminating as soon as you've covered all points (that is, all occupied grid points). Note that the last obtained digit that way is always a $1$.

Now reverse that bit string. This ensures the first it is always $1$, and therefore you can interpret the bit string as binary representation of a natural number, thus getting a bijection between point configurations and natural numbers.

Now all that remains is to map natural numbers to words. That's a pretty standard problem, and the best way to do so depends on the typical properties of your point arrangements. For example, if your points are generally always close to the origin, then you may just convert the number to base 26, and write it down using the 26 letters of the alphabet as digits. OTOH that may be a bad strategy if your points are frequently far from the origin.