Post History

The key point here is what $m$ and $n$ represent. Why is the side length of each square $\sqrt{m^2+n^2}$? Why do they have to be less than 4? And why does the author say that swapping $m$ and $n$ gives an identical case?

**Because $m$ and $n$ are the legs of the right triangles that surround the square.**

![A square, placed on a grid, so that one of its edges spans m units vertically and n units horizontally. Dashed lines show that the same measurements are repeated on the square’s other edges.](https://math.codidact.com/uploads/bPHEFS52br3bzDW44MCTSh67)

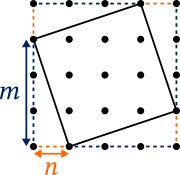
(This seems like an important detail. Maybe it’s on page 31?)

Once we know this, we can “easily see” (author’s words) that the diagonal square is contained within a larger, axis-aligned square that has side length $m+n$, and so any combination where $m+n>4$ can’t fit on the grid.