Post History
#2: Post edited
by
DNB
·
2022-01-24T08:03:34Z (about 2 years ago)
>Problem 2.4: How many squares of any size can be formed by connecting dot sin the grid shown in Figure 2.2.- I skip p 31, but apprise me if you want me to include it.
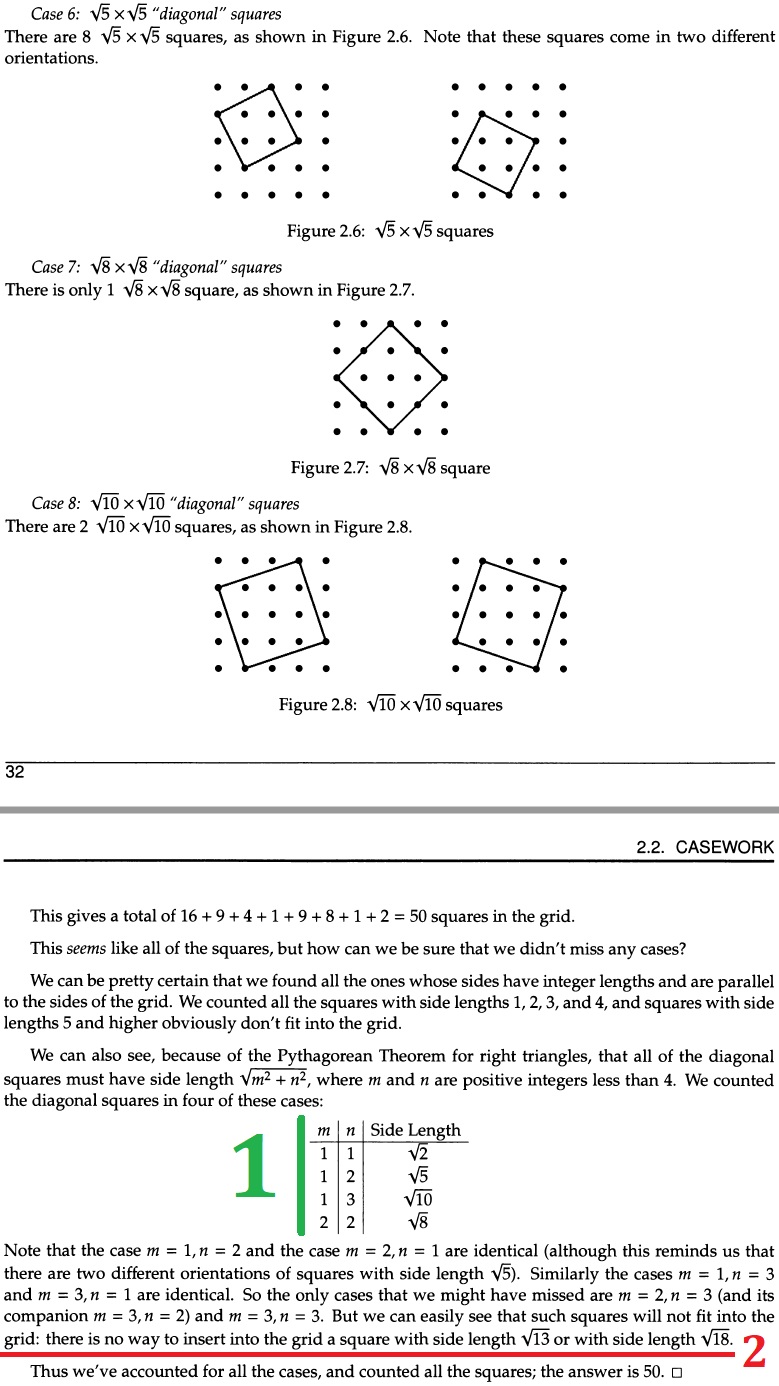
- 1. Side lengths of squares must be equal. Thus how can $m \neq n$ below?
- 2. How do you most "easily see that such squares will not fit into the grid: there is no way to insert into the grid a square with side length $\sqrt(13)$ or with side length $\sqrt(18)$"? I can't easily see this. Perhaps I need an eye exam!
- 
- David Patrick, [BS Math & Computer Science, MS Math (Carnegie Mellon), PhD Math (MIT)](https://artofproblemsolving.com/wiki/index.php/David_Patrick). *Introduction to Counting & Probability* (2005), pp 30, 32-3.
- >Problem 2.4: How many squares of any size can be formed by connecting dots in the grid shown in Figure 2.2.
- I skip p 31, but apprise me if you want me to include it.
- 1. Side lengths of squares must be equal. Thus how can $m \neq n$ below?
- 2. How do you most "easily see that such squares will not fit into the grid: there is no way to insert into the grid a square with side length $\sqrt(13)$ or with side length $\sqrt(18)$"? I can't easily see this. Perhaps I need an eye exam!
- 
- David Patrick, [BS Math & Computer Science, MS Math (Carnegie Mellon), PhD Math (MIT)](https://artofproblemsolving.com/wiki/index.php/David_Patrick). *Introduction to Counting & Probability* (2005), pp 30, 32-3.
#1: Initial revision
by
DNB
·
2022-01-24T03:45:23Z (about 2 years ago)
How can you "easily see that such squares [of side length $\sqrt{13}$ and $\sqrt{18}$] will not fit into the [4 × 4] grid"?
>Problem 2.4: How many squares of any size can be formed by connecting dot sin the grid shown in Figure 2.2. I skip p 31, but apprise me if you want me to include it. 1. Side lengths of squares must be equal. Thus how can $m \neq n$ below? 2. How do you most "easily see that such squares will not fit into the grid: there is no way to insert into the grid a square with side length $\sqrt(13)$ or with side length $\sqrt(18)$"? I can't easily see this. Perhaps I need an eye exam!  David Patrick, [BS Math & Computer Science, MS Math (Carnegie Mellon), PhD Math (MIT)](https://artofproblemsolving.com/wiki/index.php/David_Patrick). *Introduction to Counting & Probability* (2005), pp 30, 32-3.