Post History
#3: Post edited
- Where did $\color{red}{p_n = \frac16 (p_{n-1} + p_{n-2} + p_{n-3} + p_{n-4} + p_{n-5} + p_{n-6})}$ spring from? The solution doesn't expatiate, and makes it appear out of the blue? Can you please familiarize and naturalize me with this?
- Calculating [$p_1, ..., p_6$](https://math.stackexchange.com/a/1867989) — as [John](https://math.stackexchange.com/users/7163/john) did — failed to uncover the recursive equation, and led him astray to a formula containing a combinatorial coefficient instead!
- >48. A fair die is rolled repeatedly, and a running total is kept (which is, at each time, the total of all the rolls up until that time). Let $p_n$ be the probability that the running total is ever exactly n (assume the die will always be rolled enough times so that the running total will eventually exceed n, but it may or may not ever equal n).
- >
- >(a) Write down a recursive equation for $p_n$ (relating $p_n$ to earlier terms $p_k$ in a simple way). Your equation should be true for all positive integers n, so give a definition of $p_0$ and $p_k$ for $k < 0$ so that the recursive equation is true for small values of n.
- >
- >(b) Find $p_7$.
- >
- >(c) Give an intuitive explanation for the fact that $p_n \rightarrow 1/3.5=2/7$ as $n \rightarrow \infty$.
- >
- >### Solution:
- >
- >(a) We will find something to condition on to reduce the case of interest to earlier,
- simpler cases. This is achieved by the useful strategy of *first step analysis*. Let $p_n$ be the
- probability that the running total is ever *exactly n*. Note that if, for example, the first throw is a 3, then the probability of reaching n exactly is $p{n_3}$ since starting from that point, we need to get a total of $n-3$ exactly. So
- $\color{red}{p_n = \frac16 (p_{n-1} + p_{n-2} + p_{n-3} + p_{n-4} + p_{n-5} + p_{n-6})}$;
- where we define $p_0 = 1$ (which makes sense anyway since the running total is 0 before the first toss) and $p_k = 0$ for $k < 0$.
- Blitzstein, *Introduction to Probability* (2019 2 edn), Chapter 2, Exercise 48, p 94.
- pp 16-7 in the publicly downloadable PDF of curbed solutions.
- Where did $\color{red}{p_n = \frac16 (p_{n-1} + p_{n-2} + p_{n-3} + p_{n-4} + p_{n-5} + p_{n-6})}$ spring from? The solution doesn't expatiate, and makes it appear out of the blue? Can you please familiarize and naturalize me with this?
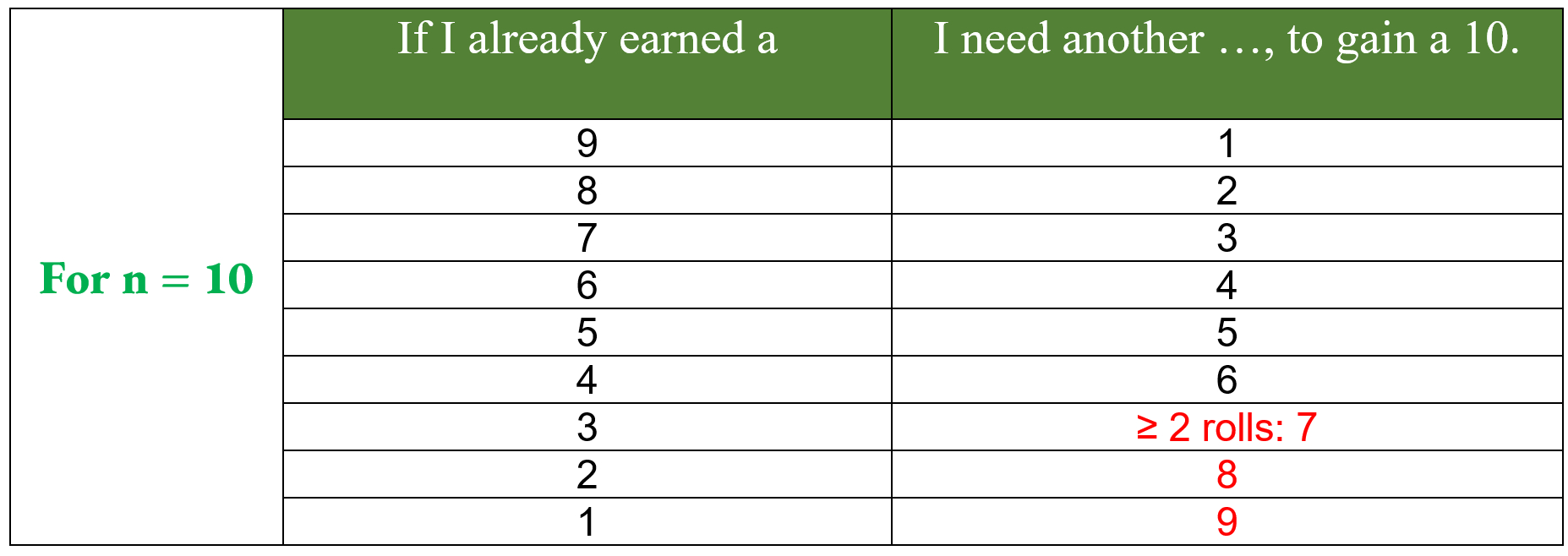
- I've tried to contemplate the ways that rolling can sum to $n$. For example, how can I roll to 10 in terms of previous rolls?
- 
- Calculating [$p_1, ..., p_6$](https://math.stackexchange.com/a/1867989) — as [John](https://math.stackexchange.com/users/7163/john) did — failed to uncover the recursive equation, and led him astray to a formula containing a combinatorial coefficient instead!
- >48. A fair die is rolled repeatedly, and a running total is kept (which is, at each time, the total of all the rolls up until that time). Let $p_n$ be the probability that the running total is ever exactly n (assume the die will always be rolled enough times so that the running total will eventually exceed n, but it may or may not ever equal n).
- >
- >(a) Write down a recursive equation for $p_n$ (relating $p_n$ to earlier terms $p_k$ in a simple way). Your equation should be true for all positive integers n, so give a definition of $p_0$ and $p_k$ for $k < 0$ so that the recursive equation is true for small values of n.
- >
- >(b) Find $p_7$.
- >
- >(c) Give an intuitive explanation for the fact that $p_n \rightarrow 1/3.5=2/7$ as $n \rightarrow \infty$.
- >
- >### Solution:
- >
- >(a) We will find something to condition on to reduce the case of interest to earlier,
- simpler cases. This is achieved by the useful strategy of *first step analysis*. Let $p_n$ be the
- probability that the running total is ever *exactly n*. Note that if, for example, the first throw is a 3, then the probability of reaching n exactly is $p{n_3}$ since starting from that point, we need to get a total of $n-3$ exactly. So
- $\color{red}{p_n = \frac16 (p_{n-1} + p_{n-2} + p_{n-3} + p_{n-4} + p_{n-5} + p_{n-6})}$;
- where we define $p_0 = 1$ (which makes sense anyway since the running total is 0 before the first toss) and $p_k = 0$ for $k < 0$.
- Blitzstein, *Introduction to Probability* (2019 2 edn), Chapter 2, Exercise 48, p 94.
- pp 16-7 in the publicly downloadable PDF of curbed solutions.
#2: Post edited
- Where did $\color{red}{p_n = \frac16 (p_{n-1} + p_{n-2} + p_{n-3} + p_{n-4} + p_{n-5} + p_{n-6})}$ spring from? The solution doesn't expatiate, and makes it appear out of the blue? Can you please familiarize and naturalize me with this?
- >48. A fair die is rolled repeatedly, and a running total is kept (which is, at each time, the total of all the rolls up until that time). Let $p_n$ be the probability that the running total is ever exactly n (assume the die will always be rolled enough times so that the running total will eventually exceed n, but it may or may not ever equal n).
- >
- >(a) Write down a recursive equation for $p_n$ (relating $p_n$ to earlier terms $p_k$ in a simple way). Your equation should be true for all positive integers n, so give a definition of $p_0$ and $p_k$ for $k < 0$ so that the recursive equation is true for small values of n.
- >
- >(b) Find $p_7$.
- >
- >(c) Give an intuitive explanation for the fact that $p_n \rightarrow 1/3.5=2/7$ as $n \rightarrow \infty$.
- >
- >### Solution:
- >
- >(a) We will find something to condition on to reduce the case of interest to earlier,
- simpler cases. This is achieved by the useful strategy of *first step analysis*. Let $p_n$ be the
- probability that the running total is ever *exactly n*. Note that if, for example, the first throw is a 3, then the probability of reaching n exactly is $p{n_3}$ since starting from that point, we need to get a total of $n-3$ exactly. So
- $\color{red}{p_n = \frac16 (p_{n-1} + p_{n-2} + p_{n-3} + p_{n-4} + p_{n-5} + p_{n-6})}$;
- where we define $p_0 = 1$ (which makes sense anyway since the running total is 0 before the first toss) and $p_k = 0$ for $k < 0$.
- Blitzstein, *Introduction to Probability* (2019 2 edn), Chapter 2, Exercise 48, p 94.
- pp 16-7 in the publicly downloadable PDF of curbed solutions.
- Where did $\color{red}{p_n = \frac16 (p_{n-1} + p_{n-2} + p_{n-3} + p_{n-4} + p_{n-5} + p_{n-6})}$ spring from? The solution doesn't expatiate, and makes it appear out of the blue? Can you please familiarize and naturalize me with this?
- Calculating [$p_1, ..., p_6$](https://math.stackexchange.com/a/1867989) — as [John](https://math.stackexchange.com/users/7163/john) did — failed to uncover the recursive equation, and led him astray to a formula containing a combinatorial coefficient instead!
- >48. A fair die is rolled repeatedly, and a running total is kept (which is, at each time, the total of all the rolls up until that time). Let $p_n$ be the probability that the running total is ever exactly n (assume the die will always be rolled enough times so that the running total will eventually exceed n, but it may or may not ever equal n).
- >
- >(a) Write down a recursive equation for $p_n$ (relating $p_n$ to earlier terms $p_k$ in a simple way). Your equation should be true for all positive integers n, so give a definition of $p_0$ and $p_k$ for $k < 0$ so that the recursive equation is true for small values of n.
- >
- >(b) Find $p_7$.
- >
- >(c) Give an intuitive explanation for the fact that $p_n \rightarrow 1/3.5=2/7$ as $n \rightarrow \infty$.
- >
- >### Solution:
- >
- >(a) We will find something to condition on to reduce the case of interest to earlier,
- simpler cases. This is achieved by the useful strategy of *first step analysis*. Let $p_n$ be the
- probability that the running total is ever *exactly n*. Note that if, for example, the first throw is a 3, then the probability of reaching n exactly is $p{n_3}$ since starting from that point, we need to get a total of $n-3$ exactly. So
- $\color{red}{p_n = \frac16 (p_{n-1} + p_{n-2} + p_{n-3} + p_{n-4} + p_{n-5} + p_{n-6})}$;
- where we define $p_0 = 1$ (which makes sense anyway since the running total is 0 before the first toss) and $p_k = 0$ for $k < 0$.
- Blitzstein, *Introduction to Probability* (2019 2 edn), Chapter 2, Exercise 48, p 94.
- pp 16-7 in the publicly downloadable PDF of curbed solutions.
#1: Initial revision
Why's Pr(the running total of a fair dice rolled repeatedly = n) = $\frac16 (p_{n-1} + p_{n-2} + p_{n-3} + p_{n-4} + p_{n-5} + p_{n-6})$?
Where did $\color{red}{p_n = \frac16 (p_{n-1} + p_{n-2} + p_{n-3} + p_{n-4} + p_{n-5} + p_{n-6})}$ spring from? The solution doesn't expatiate, and makes it appear out of the blue? Can you please familiarize and naturalize me with this?
>48. A fair die is rolled repeatedly, and a running total is kept (which is, at each time, the total of all the rolls up until that time). Let $p_n$ be the probability that the running total is ever exactly n (assume the die will always be rolled enough times so that the running total will eventually exceed n, but it may or may not ever equal n).
>
>(a) Write down a recursive equation for $p_n$ (relating $p_n$ to earlier terms $p_k$ in a simple way). Your equation should be true for all positive integers n, so give a definition of $p_0$ and $p_k$ for $k < 0$ so that the recursive equation is true for small values of n.
>
>(b) Find $p_7$.
>
>(c) Give an intuitive explanation for the fact that $p_n \rightarrow 1/3.5=2/7$ as $n \rightarrow \infty$.
>
>### Solution:
>
>(a) We will find something to condition on to reduce the case of interest to earlier,
simpler cases. This is achieved by the useful strategy of *first step analysis*. Let $p_n$ be the
probability that the running total is ever *exactly n*. Note that if, for example, the first throw is a 3, then the probability of reaching n exactly is $p{n_3}$ since starting from that point, we need to get a total of $n-3$ exactly. So
$\color{red}{p_n = \frac16 (p_{n-1} + p_{n-2} + p_{n-3} + p_{n-4} + p_{n-5} + p_{n-6})}$;
where we define $p_0 = 1$ (which makes sense anyway since the running total is 0 before the first toss) and $p_k = 0$ for $k < 0$.
Blitzstein, *Introduction to Probability* (2019 2 edn), Chapter 2, Exercise 48, p 94.
pp 16-7 in the publicly downloadable PDF of curbed solutions.


















