Post History
#2: Post edited
by
DNB
·
2022-01-17T08:54:19Z (almost 3 years ago)
- 1. Why can this problem "be thought of as a gambler's ruin where each player starts out
- with $2"?
- 2. Please see my red arrow. Why is this exponent 4? I quote op. cit. p 73.
>**Example 2.7.3** (Gambler's ruin). Two gamblers, A and B, make a sequence of \$1 bets. In each bet, gambler A has probability p of winning, and gambler B has probability $q = 1-p$ of winning. Gambler A starts with i dollars and gambler B- starts with $N-i$ dollars; the total wealth between the two remains constant since every time A loses a dollar, the dollar goes to B, and vice versa.
- >
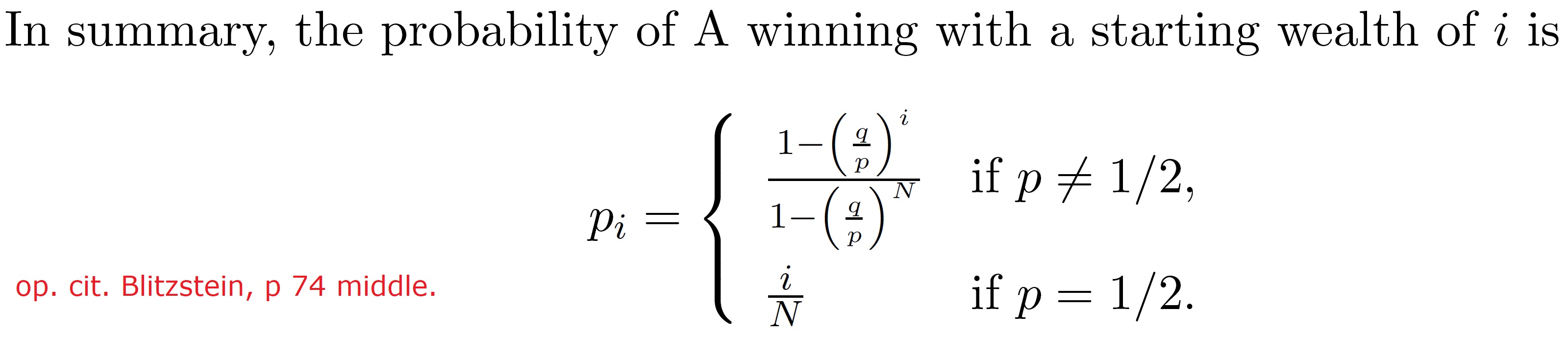
- >50. Calvin and Hobbes play a match consisting of a series of games, where Calvin has
- probability p of winning each game (independently). They play with a "win by two" rule: the first player to win two games more than his opponent wins the match. Find
- the probability that Calvin wins the match (in terms of p), in two different ways:
- >
- >(a) by conditioning, using the law of total probability.
- >
- >(b) by interpreting the problem as a gambler's ruin problem.
- >
- >## Solution:
- >
- >(b) The problem can be thought of as a gambler's ruin where each player starts out
- with $2. So the probability that Calvin wins the match is
- >
- >
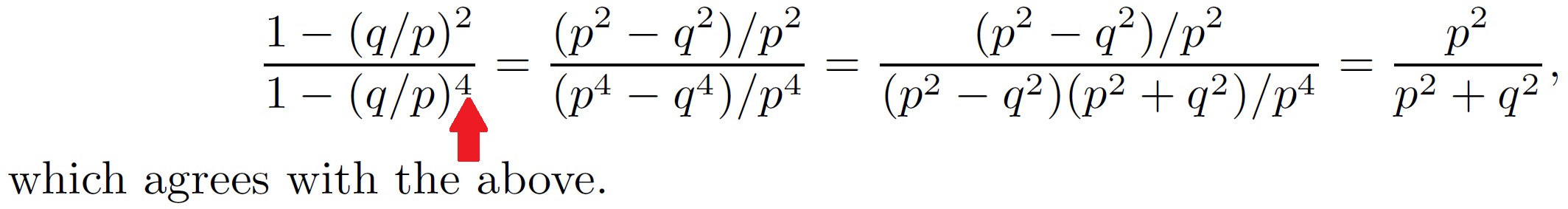
- Blitzstein, *Introduction to Probability* (2019 2 edn), Chapter 2, Exercise 50, p 94.
- p 18 in the publicly downloadable PDF of curbed solutions.
- 1. Why can this problem "be thought of as a gambler's ruin where each player starts out
- with $2"?
- 2. Please see my red arrow. Why is this exponent 4? I quote op. cit. p 73.
- >**Example 2.7.3** (Gambler's ruin). Two gamblers, A and B, make a sequence of \\$1 bets. In each bet, gambler A has probability p of winning, and gambler B has probability $q = 1-p$ of winning. Gambler A starts with $i$ dollars and gambler B
- starts with $N-i$ dollars; the total wealth between the two remains constant since every time A loses a dollar, the dollar goes to B, and vice versa.
- >
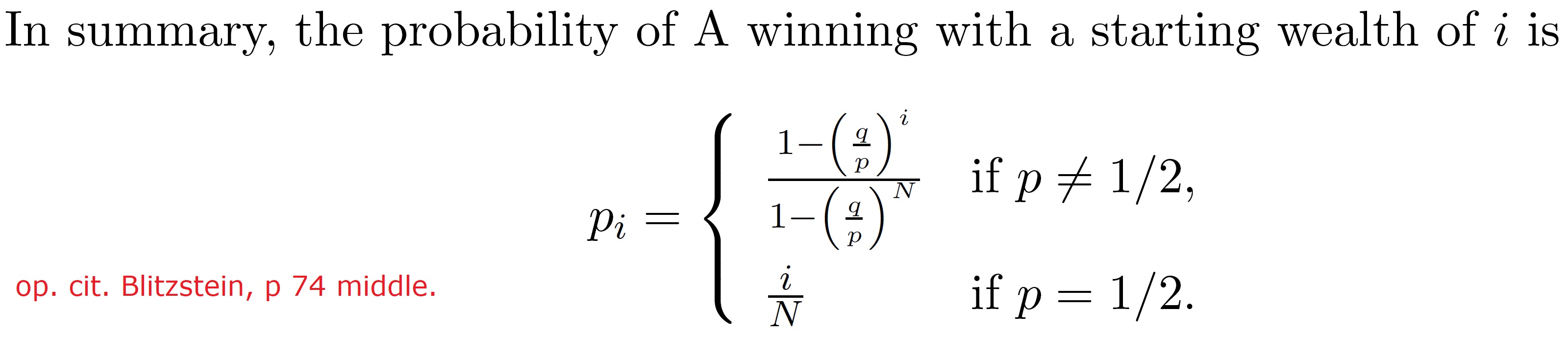
- >50. Calvin and Hobbes play a match consisting of a series of games, where Calvin has
- probability p of winning each game (independently). They play with a "win by two" rule: the first player to win two games more than his opponent wins the match. Find
- the probability that Calvin wins the match (in terms of p), in two different ways:
- >
- >(a) by conditioning, using the law of total probability.
- >
- >(b) by interpreting the problem as a gambler's ruin problem.
- >
- >## Solution:
- >
- >(b) The problem can be thought of as a gambler's ruin where each player starts out
- with $2. So the probability that Calvin wins the match is
- >
- >
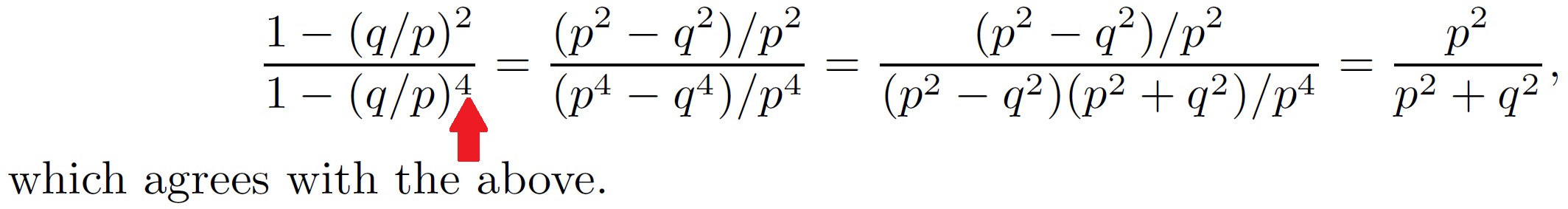
- Blitzstein, *Introduction to Probability* (2019 2 edn), Chapter 2, Exercise 50, p 94.
- p 18 in the publicly downloadable PDF of curbed solutions.
#1: Initial revision
by
DNB
·
2021-12-31T08:41:57Z (almost 3 years ago)
Why's a 2-player game with "win by two" rule = Gambler's Ruin where each player starts with $2? Why N = 4?
1. Why can this problem "be thought of as a gambler's ruin where each player starts out with $2"? 2. Please see my red arrow. Why is this exponent 4? I quote op. cit. p 73. >**Example 2.7.3** (Gambler's ruin). Two gamblers, A and B, make a sequence of \$1 bets. In each bet, gambler A has probability p of winning, and gambler B has probability $q = 1-p$ of winning. Gambler A starts with i dollars and gambler B starts with $N-i$ dollars; the total wealth between the two remains constant since every time A loses a dollar, the dollar goes to B, and vice versa. >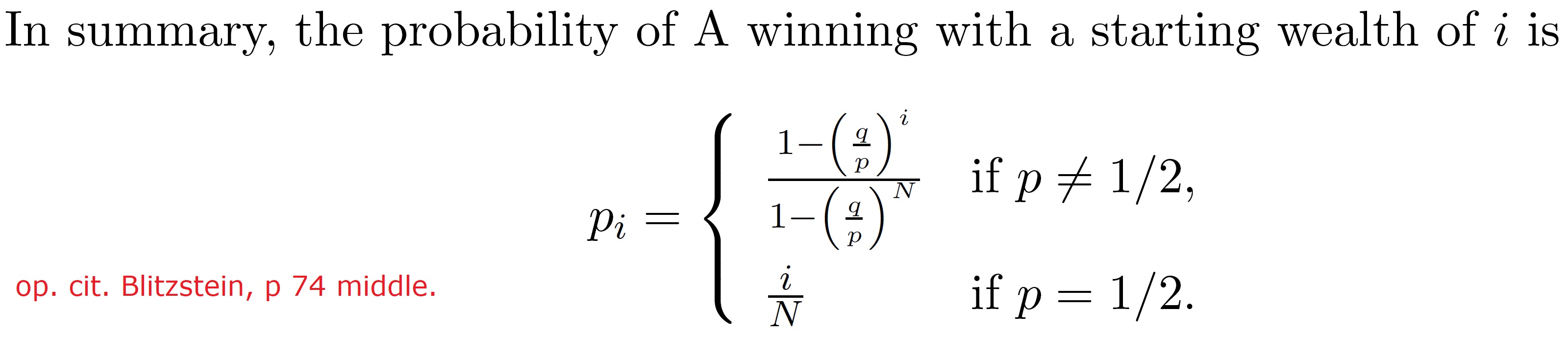 >50. Calvin and Hobbes play a match consisting of a series of games, where Calvin has probability p of winning each game (independently). They play with a "win by two" rule: the first player to win two games more than his opponent wins the match. Find the probability that Calvin wins the match (in terms of p), in two different ways: > >(a) by conditioning, using the law of total probability. > >(b) by interpreting the problem as a gambler's ruin problem. > >## Solution: > >(b) The problem can be thought of as a gambler's ruin where each player starts out with $2. So the probability that Calvin wins the match is > >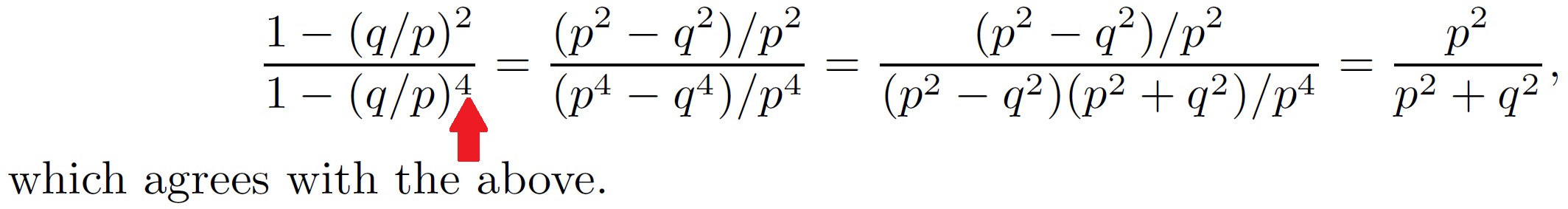 Blitzstein, *Introduction to Probability* (2019 2 edn), Chapter 2, Exercise 50, p 94. p 18 in the publicly downloadable PDF of curbed solutions.