Post History

71%

+3 −0

Q&A Find limits of integration in polar coordinates

2 answers · posted 3y ago by MissMulan‭ · last activity 3y ago by r~~‭

Question calculus double-integrals polar

#2: Post edited by (deleted user) · 2021-08-24T15:41:41Z (over 3 years ago)
more better alt text

Copy Link

Raw

Markdown

Find limits of integration in polar coordinates

Suppose we have this graph and we want to find the area between the 2 curves:
![hi](https://math.codidact.com/uploads/xum62GPERZqYiqMuiVmgLAq1).
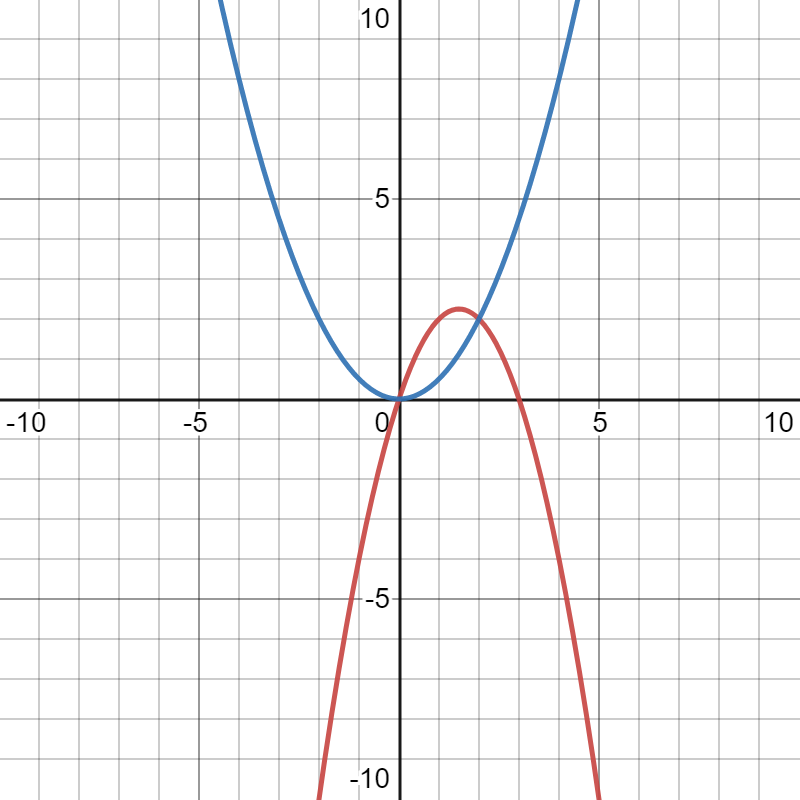We can calculate the are using a double integral:
~~![hi](https://math.codidact.com/uploads/axR3bn8H6att46y116XAXeUT)~~
~~![hi](https://math.codidact.com/uploads/yk94caT3ihKQs4P9nCVwGWhb)~~
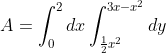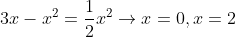In polar coordinates the equation of the curves take this form:
~~![a](https://math.codidact.com/uploads/odkFguKn7CnqsyLG3QMDFBvY)~~
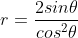and
~~![a](https://math.codidact.com/uploads/u7BqhyH2viMsy5AZHBoquKEC)~~
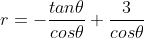How do I find the limits of integration of the angle theta?

Suppose we have this graph and we want to find the area between the 2 curves:
![hi](https://math.codidact.com/uploads/xum62GPERZqYiqMuiVmgLAq1).
We can calculate the are using a double integral:
![graph](https://math.codidact.com/uploads/axR3bn8H6att46y116XAXeUT)
![equation](https://math.codidact.com/uploads/yk94caT3ihKQs4P9nCVwGWhb)
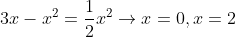
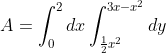
In polar coordinates the equation of the curves take this form:
![equation](https://math.codidact.com/uploads/odkFguKn7CnqsyLG3QMDFBvY)
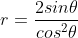
and
![equation](https://math.codidact.com/uploads/u7BqhyH2viMsy5AZHBoquKEC)
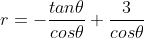
How do I find the limits of integration of the angle theta?

#1: Initial revision by $user avatar$ MissMulan‭ · 2021-08-24T13:36:10Z (over 3 years ago)

Copy Link

Raw

Markdown

Find limits of integration in polar coordinates

Suppose we have this graph and we want to find the area between the 2 curves:

![hi](https://math.codidact.com/uploads/xum62GPERZqYiqMuiVmgLAq1).

We can calculate the are using a double integral: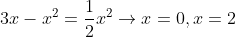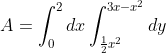

![hi](https://math.codidact.com/uploads/axR3bn8H6att46y116XAXeUT)

![hi](https://math.codidact.com/uploads/yk94caT3ihKQs4P9nCVwGWhb)

In polar coordinates the equation of the curves take this form: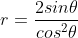

![a](https://math.codidact.com/uploads/odkFguKn7CnqsyLG3QMDFBvY)

and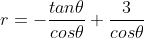 

![a](https://math.codidact.com/uploads/u7BqhyH2viMsy5AZHBoquKEC)

How do I find the limits of integration of the angle theta?

calculus double-integrals polar

Communities

Post History