Post History
#3: Post edited
by
celtschk
·
2021-08-08T05:55:51Z (over 3 years ago)
Fixed a typo
- The correct equation for the square boundary you sketched is
- $$\left|x\right| + \left|y\right| = 5$$
- where $\left|x\right|$ means the absolute value of $x$, that is,
- $$\left|x\right| =
- \begin{cases}
- x & \text{for $x\ge 0$}\\\\
- -x & \text{for $x < 0$}
- \end{cases}$$
- Now to calculate the area with calculus, the easiest way to do so is to first note that the square is composed of four congruent triangles corresponding to the sign choices of $x$ and $y$. Therefore you can calculate the area of one of those triangles and multiply the result by $4$.
- The obvious choice is the triangle where $x$ and $y$ are both positive, because there you can simply omit the absolute value bars, so you get $x+y=5$ or solved for $y$,
- $$y = 5 - x$$
- Since you are now only looking at the positive values of $x$, your integration goes only from $0$ to $5$, so the area of the triangle is
- $$A_\triangle = \int_0^5 (5-x) \\,\mathrm dx = \frac{25}{2}$$
- Therefore we get for the total area of the square
- $$A_\square = 4 A_\triangle = 50$$
- which indeed is the correct area of the square.
- Note that while your last calculation also gives the value $50$, this is a coincidence. What you actually calculated there is the area of the equilateral right triangle that sits above the $x$-axis with the right angle at the left side, and going up to $10$ on the left side. It is easy to see geometrically that this has the same area as the square (half of it is the upper half of the square, and the other half is congruent to the lower half of the square).
- To see how the square has area $50$, the following image should help:
- 
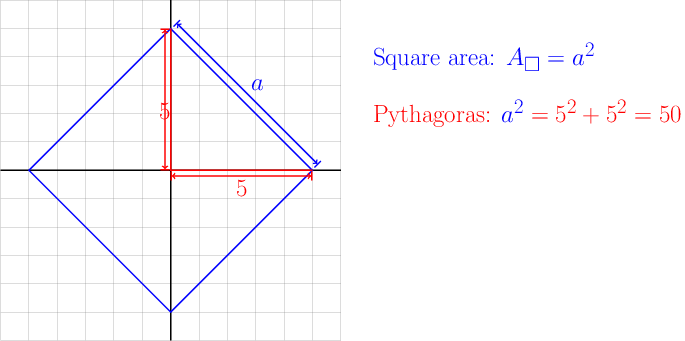
The square, drawn in blue, has corners $(0,5)$, $(5,0)$, $(0,-5)$ and $(-5,0)$. The sides are connecting those points, and are of course all of equal length, which I names $a$.- The length of this side can be obtained by noting that the triangle formed by the origin and the two end points of the square side is a right triangle, with the right angle at the origin, and therefore Pythagoras can be used. The two triangle sides at that right angle have both length $5$ (since they go from $(0,0)$ to either $(0,\pm 5)$. The triangle side opposite to the right angle is the side of the square whose length $a$ we want to determine, and Pythagoras tells us that
- $$a^2 = 5^2+5^2 = 50$$
- Now the area of the square is, of course, $A_\square = a^2$, therefore inserting the above result gives
- $$A_\square = 50$$
- Note that the right triangle is exactly the quarter-square whose area was calculated with the integral above. Another geometric way to determine the area therefore is to calculate the area of that right triangle by taking one of the sides going to the right angle as base line, and noting that the other one then is the height. Therefore the area of that triangle is
- $$A_\triangle = \frac12 b h = \frac12\cdot 5\cdot 5 = \frac{25}{2}$$
- and then
- $$A_\square = 4A\triangle = 50$$
- The correct equation for the square boundary you sketched is
- $$\left|x\right| + \left|y\right| = 5$$
- where $\left|x\right|$ means the absolute value of $x$, that is,
- $$\left|x\right| =
- \begin{cases}
- x & \text{for $x\ge 0$}\\\\
- -x & \text{for $x < 0$}
- \end{cases}$$
- Now to calculate the area with calculus, the easiest way to do so is to first note that the square is composed of four congruent triangles corresponding to the sign choices of $x$ and $y$. Therefore you can calculate the area of one of those triangles and multiply the result by $4$.
- The obvious choice is the triangle where $x$ and $y$ are both positive, because there you can simply omit the absolute value bars, so you get $x+y=5$ or solved for $y$,
- $$y = 5 - x$$
- Since you are now only looking at the positive values of $x$, your integration goes only from $0$ to $5$, so the area of the triangle is
- $$A_\triangle = \int_0^5 (5-x) \\,\mathrm dx = \frac{25}{2}$$
- Therefore we get for the total area of the square
- $$A_\square = 4 A_\triangle = 50$$
- which indeed is the correct area of the square.
- Note that while your last calculation also gives the value $50$, this is a coincidence. What you actually calculated there is the area of the equilateral right triangle that sits above the $x$-axis with the right angle at the left side, and going up to $10$ on the left side. It is easy to see geometrically that this has the same area as the square (half of it is the upper half of the square, and the other half is congruent to the lower half of the square).
- To see how the square has area $50$, the following image should help:
- 
- The square, drawn in blue, has corners $(0,5)$, $(5,0)$, $(0,-5)$ and $(-5,0)$. The sides are connecting those points, and are of course all of equal length, which I named $a$.
- The length of this side can be obtained by noting that the triangle formed by the origin and the two end points of the square side is a right triangle, with the right angle at the origin, and therefore Pythagoras can be used. The two triangle sides at that right angle have both length $5$ (since they go from $(0,0)$ to either $(0,\pm 5)$. The triangle side opposite to the right angle is the side of the square whose length $a$ we want to determine, and Pythagoras tells us that
- $$a^2 = 5^2+5^2 = 50$$
- Now the area of the square is, of course, $A_\square = a^2$, therefore inserting the above result gives
- $$A_\square = 50$$
- Note that the right triangle is exactly the quarter-square whose area was calculated with the integral above. Another geometric way to determine the area therefore is to calculate the area of that right triangle by taking one of the sides going to the right angle as base line, and noting that the other one then is the height. Therefore the area of that triangle is
- $$A_\triangle = \frac12 b h = \frac12\cdot 5\cdot 5 = \frac{25}{2}$$
- and then
- $$A_\square = 4A\triangle = 50$$
#2: Post edited
by
celtschk
·
2021-08-08T05:53:49Z (over 3 years ago)
Added explannation why the area of the square is, indeed, 50
- The correct equation for the square boundary you sketched is
- $$\left|x\right| + \left|y\right| = 5$$
- where $\left|x\right|$ means the absolute value of $x$, that is,
- $$\left|x\right| =
- \begin{cases}
- x & \text{for $x\ge 0$}\\\\
- -x & \text{for $x < 0$}
- \end{cases}$$
- Now to calculate the area with calculus, the easiest way to do so is to first note that the square is composed of four congruent triangles corresponding to the sign choices of $x$ and $y$. Therefore you can calculate the area of one of those triangles and multiply the result by $4$.
- The obvious choice is the triangle where $x$ and $y$ are both positive, because there you can simply omit the absolute value bars, so you get $x+y=5$ or solved for $y$,
- $$y = 5 - x$$
- Since you are now only looking at the positive values of $x$, your integration goes only from $0$ to $5$, so the area of the triangle is
- $$A_\triangle = \int_0^5 (5-x) \\,\mathrm dx = \frac{25}{2}$$
- Therefore we get for the total area of the square
- $$A_\square = 4 A_\triangle = 50$$
- which indeed is the correct area of the square.
- Note that while your last calculation also gives the value $50$, this is a coincidence. What you actually calculated there is the area of the equilateral right triangle that sits above the $x$-axis with the right angle at the left side, and going up to $10$ on the left side. It is easy to see geometrically that this has the same area as the square (half of it is the upper half of the square, and the other half is congruent to the lower half of the square).
- The correct equation for the square boundary you sketched is
- $$\left|x\right| + \left|y\right| = 5$$
- where $\left|x\right|$ means the absolute value of $x$, that is,
- $$\left|x\right| =
- \begin{cases}
- x & \text{for $x\ge 0$}\\\\
- -x & \text{for $x < 0$}
- \end{cases}$$
- Now to calculate the area with calculus, the easiest way to do so is to first note that the square is composed of four congruent triangles corresponding to the sign choices of $x$ and $y$. Therefore you can calculate the area of one of those triangles and multiply the result by $4$.
- The obvious choice is the triangle where $x$ and $y$ are both positive, because there you can simply omit the absolute value bars, so you get $x+y=5$ or solved for $y$,
- $$y = 5 - x$$
- Since you are now only looking at the positive values of $x$, your integration goes only from $0$ to $5$, so the area of the triangle is
- $$A_\triangle = \int_0^5 (5-x) \\,\mathrm dx = \frac{25}{2}$$
- Therefore we get for the total area of the square
- $$A_\square = 4 A_\triangle = 50$$
- which indeed is the correct area of the square.
- Note that while your last calculation also gives the value $50$, this is a coincidence. What you actually calculated there is the area of the equilateral right triangle that sits above the $x$-axis with the right angle at the left side, and going up to $10$ on the left side. It is easy to see geometrically that this has the same area as the square (half of it is the upper half of the square, and the other half is congruent to the lower half of the square).
- To see how the square has area $50$, the following image should help:
- 
- The square, drawn in blue, has corners $(0,5)$, $(5,0)$, $(0,-5)$ and $(-5,0)$. The sides are connecting those points, and are of course all of equal length, which I names $a$.
- The length of this side can be obtained by noting that the triangle formed by the origin and the two end points of the square side is a right triangle, with the right angle at the origin, and therefore Pythagoras can be used. The two triangle sides at that right angle have both length $5$ (since they go from $(0,0)$ to either $(0,\pm 5)$. The triangle side opposite to the right angle is the side of the square whose length $a$ we want to determine, and Pythagoras tells us that
- $$a^2 = 5^2+5^2 = 50$$
- Now the area of the square is, of course, $A_\square = a^2$, therefore inserting the above result gives
- $$A_\square = 50$$
- Note that the right triangle is exactly the quarter-square whose area was calculated with the integral above. Another geometric way to determine the area therefore is to calculate the area of that right triangle by taking one of the sides going to the right angle as base line, and noting that the other one then is the height. Therefore the area of that triangle is
- $$A_\triangle = \frac12 b h = \frac12\cdot 5\cdot 5 = \frac{25}{2}$$
- and then
- $$A_\square = 4A\triangle = 50$$
#1: Initial revision
by
celtschk
·
2021-08-06T06:56:38Z (over 3 years ago)
The correct equation for the square boundary you sketched is
$$\left|x\right| + \left|y\right| = 5$$
where $\left|x\right|$ means the absolute value of $x$, that is,
$$\left|x\right| =
\begin{cases}
x & \text{for $x\ge 0$}\\\\
-x & \text{for $x < 0$}
\end{cases}$$
Now to calculate the area with calculus, the easiest way to do so is to first note that the square is composed of four congruent triangles corresponding to the sign choices of $x$ and $y$. Therefore you can calculate the area of one of those triangles and multiply the result by $4$.
The obvious choice is the triangle where $x$ and $y$ are both positive, because there you can simply omit the absolute value bars, so you get $x+y=5$ or solved for $y$,
$$y = 5 - x$$
Since you are now only looking at the positive values of $x$, your integration goes only from $0$ to $5$, so the area of the triangle is
$$A_\triangle = \int_0^5 (5-x) \\,\mathrm dx = \frac{25}{2}$$
Therefore we get for the total area of the square
$$A_\square = 4 A_\triangle = 50$$
which indeed is the correct area of the square.
Note that while your last calculation also gives the value $50$, this is a coincidence. What you actually calculated there is the area of the equilateral right triangle that sits above the $x$-axis with the right angle at the left side, and going up to $10$ on the left side. It is easy to see geometrically that this has the same area as the square (half of it is the upper half of the square, and the other half is congruent to the lower half of the square).