Post History
#3: Post edited
- I was studying determination of area in Calculus. So, I decided to calculate area of rectangle using Calculus.
- <hr/>
- Let, length of a line of a square is $5$. So, I decided to make an equation for that. I took $x^2+y^2=\sqrt{25}$. Firstly, it was looking perfect to me. Then, when I was calculating for $y=1$ then, I noticed I got $x=4,6$ (where 6 is wrong).
- 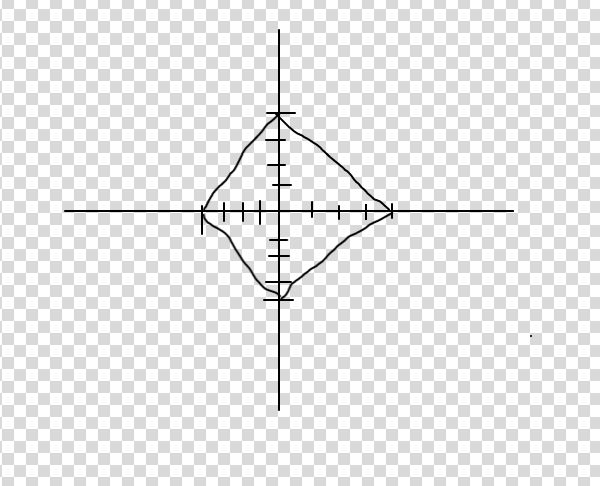
- I drew the above picture (Sorry! I don't have proper "picture" maker in system)..
- We know $$\int_{-5}^{5}y\mathrm dx$$
- $$=\int_{-5}^{5} \sqrt{\sqrt{25}-x^2}\mathrm dx$$
- If I integrate it than, I get imaginary number and infinite number. So, I think I took the wrong equation. How would you determine area of square using Integration (when length of a line is $5$)?
- **Note** : Use Cartesian Coordinate.
Ohh! Sorry. I wrote $x^2+y^2=\sqrt{25}$ but, when doing that in notepad I was doing using $x+y=\sqrt{25}$ then, I got $50$...
- I was studying determination of area in Calculus. So, I decided to calculate area of rectangle using Calculus.
- <hr/>
- Let, length of a line of a square is $5$. So, I decided to make an equation for that. I took $x^2+y^2=\sqrt{25}$. Firstly, it was looking perfect to me. Then, when I was calculating for $y=1$ then, I noticed I got $x=4,6$ (where 6 is wrong).
- 
- I drew the above picture (Sorry! I don't have proper "picture" maker in system)..
- We know $$\int_{-5}^{5}y\mathrm dx$$
- $$=\int_{-5}^{5} \sqrt{\sqrt{25}-x^2}\mathrm dx$$
- If I integrate it than, I get imaginary number and infinite number. So, I think I took the wrong equation. How would you determine area of square using Integration (when length of a line is $5$)?
- **Note** : Use Cartesian Coordinate.
- Ohh! Sorry. I wrote $x^2+y^2=\sqrt{25}$ but, when doing that in notepad I was doing using $x+y=\sqrt{25}$ then, I got $50$...
- $$\int_{-5}^{5} \sqrt{25}-x \mathrm dx$$
- $$[\sqrt{25}x]-\frac{x^2}{2}]_{-5}^5$$
- $$\sqrt{25}(5)-\sqrt{25}(-5)-\frac{25}{2}+\frac{25}{2}$$
- $$2\sqrt{25}(5)$$
- $$50,-50$$
#2: Post edited
- I was studying determination of area in Calculus. So, I decided to calculate area of rectangle using Calculus.
- <hr/>
- Let, length of a line of a square is $5$. So, I decided to make an equation for that. I took $x^2+y^2=\sqrt{25}$. Firstly, it was looking perfect to me. Then, when I was calculating for $y=1$ then, I noticed I got $x=4,6$ (where 6 is wrong).
- 
- I drew the above picture (Sorry! I don't have proper "picture" maker in system)..
- We know $$\int_{-5}^{5}y\mathrm dx$$
- $$=\int_{-5}^{5} \sqrt{\sqrt{25}-x^2}\mathrm dx$$
- If I integrate it than, I get imaginary number and infinite number. So, I think I took the wrong equation. How would you determine area of square using Integration (when length of a line is $5$)?
**Note** : Use Cartesian Coordinate.
- I was studying determination of area in Calculus. So, I decided to calculate area of rectangle using Calculus.
- <hr/>
- Let, length of a line of a square is $5$. So, I decided to make an equation for that. I took $x^2+y^2=\sqrt{25}$. Firstly, it was looking perfect to me. Then, when I was calculating for $y=1$ then, I noticed I got $x=4,6$ (where 6 is wrong).
- 
- I drew the above picture (Sorry! I don't have proper "picture" maker in system)..
- We know $$\int_{-5}^{5}y\mathrm dx$$
- $$=\int_{-5}^{5} \sqrt{\sqrt{25}-x^2}\mathrm dx$$
- If I integrate it than, I get imaginary number and infinite number. So, I think I took the wrong equation. How would you determine area of square using Integration (when length of a line is $5$)?
- **Note** : Use Cartesian Coordinate.
- Ohh! Sorry. I wrote $x^2+y^2=\sqrt{25}$ but, when doing that in notepad I was doing using $x+y=\sqrt{25}$ then, I got $50$...
#1: Initial revision
How to determine area of square using Calculus in Cartesian coodinate?
I was studying determination of area in Calculus. So, I decided to calculate area of rectangle using Calculus.
<hr/>
Let, length of a line of a square is $5$. So, I decided to make an equation for that. I took $x^2+y^2=\sqrt{25}$. Firstly, it was looking perfect to me. Then, when I was calculating for $y=1$ then, I noticed I got $x=4,6$ (where 6 is wrong).

I drew the above picture (Sorry! I don't have proper "picture" maker in system)..
We know $$\int_{-5}^{5}y\mathrm dx$$
$$=\int_{-5}^{5} \sqrt{\sqrt{25}-x^2}\mathrm dx$$
If I integrate it than, I get imaginary number and infinite number. So, I think I took the wrong equation. How would you determine area of square using Integration (when length of a line is $5$)?
**Note** : Use Cartesian Coordinate.


















