Post History
#2: Post edited
by
DNB
·
2021-08-10T07:20:03Z (over 2 years ago)
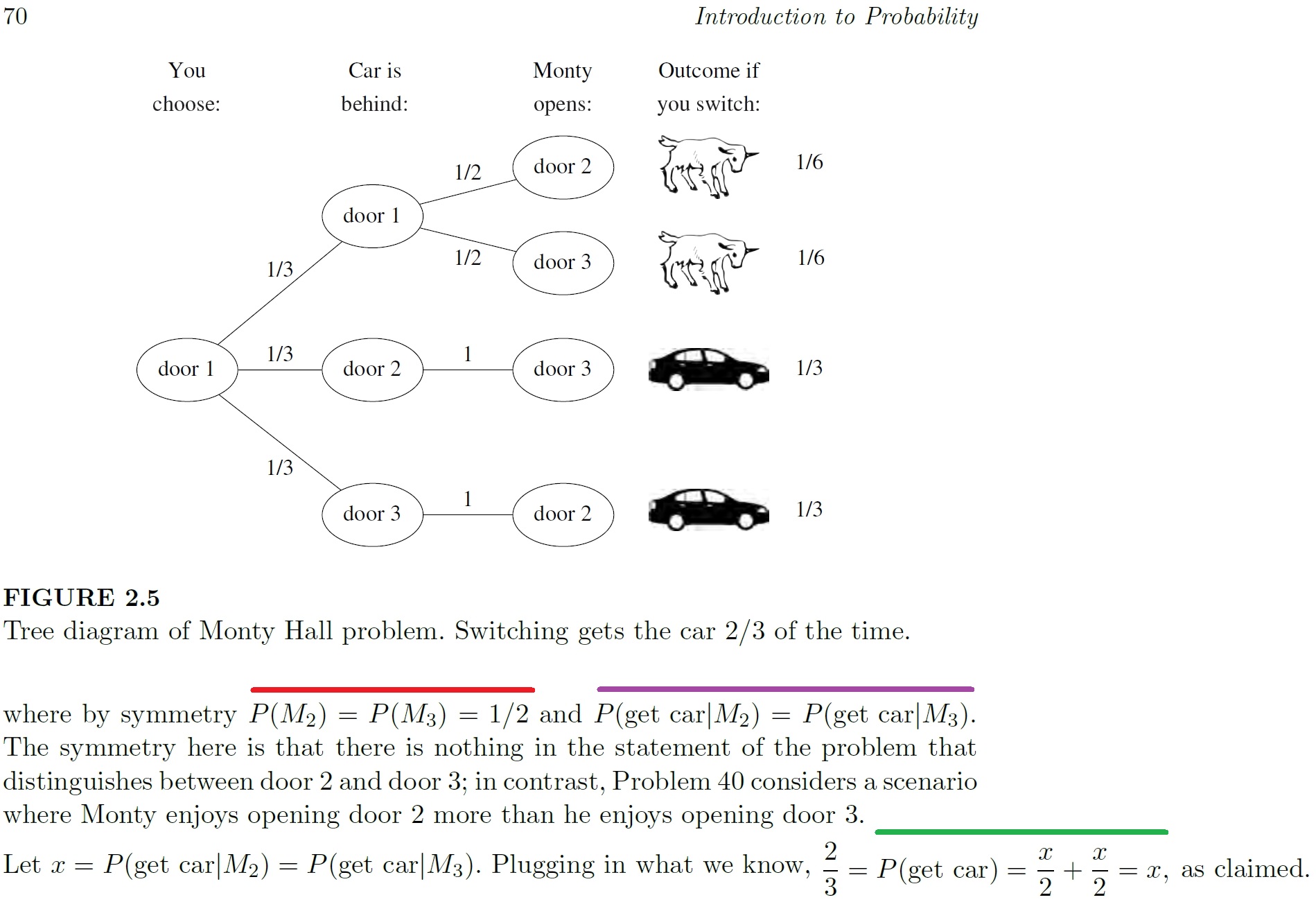
["Monty, who knows where the car is, then opens one of the two remaining doors. The door he opens always has a goat behind it (he never reveals the car!)."](https://math.codidact.com/posts/283113) So Monty must open the $M_j, j = 2,3$ with the goat, but not open the other $M_j$ with the car. So $P(M_2)eq P(M_3)$!- 1. How then $P(M_2) = P(M_3) = 1/2$ and $P(\text{get car}|M_2)P(M_2) = P(\text{get car}|M_3)P(M_3)$? Please see the sentences underlined in red and purple.
- 2. Please see the sentence underlined in green. How do you deduce the $2/3$ WITHOUT relying on the previous solution using the unconditional probability of success. Up to that sentence, you can deduce only that $P(\text{get car}) = \frac x2 + \frac x2 = x$.
- >There's a subtlety though, which is that when the contestant chooses whether to
- switch, she also knows which door Monty opened. We showed that the _unconditional_
- probability of success is 2/3 (when following the switching strategy), but let's also
- show that the _conditional_ probability of success for switching, given the information
- that Monty provides, is also 2/3.
- >Let $M_j$ be the event that Monty opens door j, for j = 2; 3. Then
- >$P(\text{get car}) = P(\text{get car}|M_2)P(M_2) + P(\text{get car}|M_3)P(M_3)$;
- 
- Blitzstein. *Introduction to Probability* (2019 2 ed). pp 69-70.
- ["Monty, who knows where the car is, then opens one of the two remaining doors. The door he opens always has a goat behind it (he never reveals the car!)."](https://math.codidact.com/posts/283113) So Monty must open ONE of the $M_j (j = 2,3$), the one with the goat! But Monty mustn't and won't open the other $M_j$ with the car. So $P(M_2)
- eq P(M_3)$!
- 1. How then $P(M_2) = P(M_3) = 1/2$ and $P(\text{get car}|M_2)P(M_2) = P(\text{get car}|M_3)P(M_3)$? Please see the sentences underlined in red and purple.
- 2. Please see the sentence underlined in green. How do you deduce the $2/3$ WITHOUT relying on the previous solution using the unconditional probability of success. Up to that sentence, you can deduce only that $P(\text{get car}) = \frac x2 + \frac x2 = x$.
- >There's a subtlety though, which is that when the contestant chooses whether to
- switch, she also knows which door Monty opened. We showed that the _unconditional_
- probability of success is 2/3 (when following the switching strategy), but let's also
- show that the _conditional_ probability of success for switching, given the information
- that Monty provides, is also 2/3.
- >Let $M_j$ be the event that Monty opens door j, for j = 2; 3. Then
- >$P(\text{get car}) = P(\text{get car}|M_2)P(M_2) + P(\text{get car}|M_3)P(M_3)$;
- 
- Blitzstein. *Introduction to Probability* (2019 2 ed). pp 69-70.
#1: Initial revision
by
DNB
·
2021-08-05T04:07:10Z (over 2 years ago)
How does P(Monty opens door 2) = P(Monty opens door 3), and $P(\text{get car}|M_2)P(M_2) = P(\text{get car}|M_3)P(M_3)$?
["Monty, who knows where the car is, then opens one of the two remaining doors. The door he opens always has a goat behind it (he never reveals the car!)."](https://math.codidact.com/posts/283113) So Monty must open the $M_j, j = 2,3$ with the goat, but not open the other $M_j$ with the car. So $P(M_2) \neq P(M_3)$!
1. How then $P(M_2) = P(M_3) = 1/2$ and $P(\text{get car}|M_2)P(M_2) = P(\text{get car}|M_3)P(M_3)$? Please see the sentences underlined in red and purple.
2. Please see the sentence underlined in green. How do you deduce the $2/3$ WITHOUT relying on the previous solution using the unconditional probability of success. Up to that sentence, you can deduce only that $P(\text{get car}) = \frac x2 + \frac x2 = x$.
>There's a subtlety though, which is that when the contestant chooses whether to
switch, she also knows which door Monty opened. We showed that the _unconditional_
probability of success is 2/3 (when following the switching strategy), but let's also
show that the _conditional_ probability of success for switching, given the information
that Monty provides, is also 2/3.
>Let $M_j$ be the event that Monty opens door j, for j = 2; 3. Then
>$P(\text{get car}) = P(\text{get car}|M_2)P(M_2) + P(\text{get car}|M_3)P(M_3)$;
Blitzstein. *Introduction to Probability* (2019 2 ed). pp 69-70.