Post History
#3: Post edited
by
Peter Taylor
·
2022-10-03T08:29:04Z (over 1 year ago)
Eliminating unhelpful tag algebra-precalculus
#2: Post edited
by
DNB
·
2021-09-18T06:35:14Z (over 2 years ago)
- This snag arose out of [this post](https://math.codidact.com/posts/282606), and [these comments by r~~](https://math.codidact.com/comments/thread/3555#comment-11900). In that post, I couldn't imagine how
- >**By convention, $n(n-1) \dots {\color{red}{(n-k+1)}} = n$ for k = 1.**
Thus I wrote out the LHS $= n(n-1) \dots (n-[k-3])(n-[k-2])\color{red}{(n-[k-1])}$. Then I substituted $k=1$ into this expression, to deduce $LHS|_{k = 1} = n(n-1) \dots (n+2)(n+1)eq n$.- But r~~ counseled that
- >[you can't simply substitute a variable into that kind of informal, descriptive expression without thinking about what the notation as a whole represents. It's not an algebraic expression, so the rules of algebra don't apply. is a signal to look at the pattern being established to the left of the dots, and extend it until it meets what is right of the dots. But if the patterns can't meet, the expression doesn't mean anything.](https://math.codidact.com/comments/thread/3555#comment-11553)
- I don't know why, but I'm unpersuaded. How does my substitution above differ from evaluating a function at an integer like the following? I can re-word my substitution above, if I define $LHS = n(n-1) \dots (n-[k-3])(n-[k-2])\color{red}{(n-[k-1])}$ as $f(n,k)$. Then I just evaluated $f(k=1)$! I see no germane difference!
- - James Stewart's _Calculus Early Transcendentals_ (2011 7e), p xxvii, Diagnostic Test C: Functions.
- 
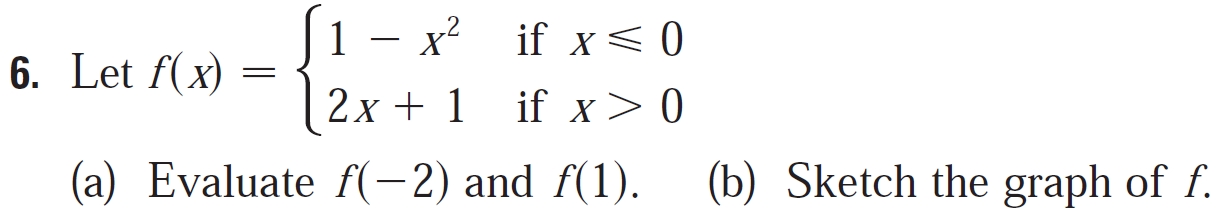
- - Ron Larson's _Calculus_ (2018 11e), p 20.
- 
- This snag arose out of [this post](https://math.codidact.com/posts/282606), and [these comments by r~~](https://math.codidact.com/comments/thread/3555#comment-11900). In that post, I couldn't imagine how
- >**By convention, $n(n-1) \dots {\color{red}{(n-k+1)}} = n$ for k = 1.**
- Thus I wrote out the LHS $= n(n-1)(n - 2) \dots (n-[k-3])(n-[k-2])\color{red}{(n-[k-1])}$. Then I substituted $k=1$ into this expression, to deduce $LHS|_
- {k = 1} = n(n-1)(n - 2) \dots (n+2)(n+1)n \quad
- eq \quad n$.
- But r~~ counseled that
- >[you can't simply substitute a variable into that kind of informal, descriptive expression without thinking about what the notation as a whole represents. It's not an algebraic expression, so the rules of algebra don't apply. is a signal to look at the pattern being established to the left of the dots, and extend it until it meets what is right of the dots. But if the patterns can't meet, the expression doesn't mean anything.](https://math.codidact.com/comments/thread/3555#comment-11553)
- I don't know why, but I'm unpersuaded. How does my substitution above differ from evaluating a function at an integer like the following? I can re-word my substitution above, if I define $LHS = n(n-1) \dots (n-[k-3])(n-[k-2])\color{red}{(n-[k-1])}$ as $f(n,k)$. Then I just evaluated $f(k=1)$! I see no germane difference!
- - James Stewart's _Calculus Early Transcendentals_ (2011 7e), p xxvii, Diagnostic Test C: Functions.
- 
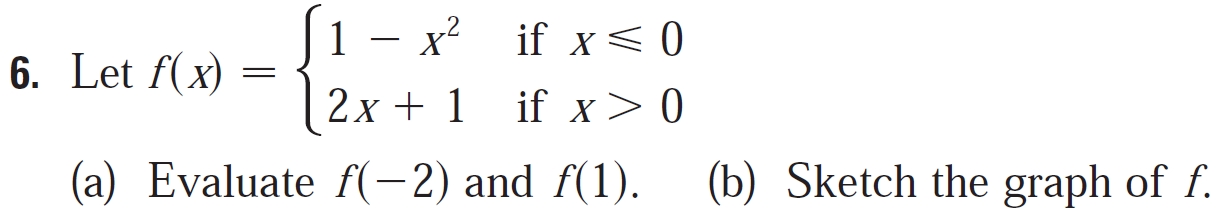
- - Ron Larson's _Calculus_ (2018 11e), p 20.
- 
#1: Initial revision
by
DNB
·
2021-07-30T02:00:37Z (over 2 years ago)
What's wrong with evaluating $n(n-1) \dots (n-[k-3])(n-[k-2])\color{red}{(n-[k-1])}$ at $k = 1$?
This snag arose out of [this post](https://math.codidact.com/posts/282606), and [these comments by r~~](https://math.codidact.com/comments/thread/3555#comment-11900). In that post, I couldn't imagine how
>**By convention, $n(n-1) \dots {\color{red}{(n-k+1)}} = n$ for k = 1.**
Thus I wrote out the LHS $= n(n-1) \dots (n-[k-3])(n-[k-2])\color{red}{(n-[k-1])}$. Then I substituted $k=1$ into this expression, to deduce $LHS|_
{k = 1} = n(n-1) \dots (n+2)(n+1) \neq n$.
But r~~ counseled that
>[you can't simply substitute a variable into that kind of informal, descriptive expression without thinking about what the notation as a whole represents. It's not an algebraic expression, so the rules of algebra don't apply. is a signal to look at the pattern being established to the left of the dots, and extend it until it meets what is right of the dots. But if the patterns can't meet, the expression doesn't mean anything.](https://math.codidact.com/comments/thread/3555#comment-11553)
I don't know why, but I'm unpersuaded. How does my substitution above differ from evaluating a function at an integer like the following? I can re-word my substitution above, if I define $LHS = n(n-1) \dots (n-[k-3])(n-[k-2])\color{red}{(n-[k-1])}$ as $f(n,k)$. Then I just evaluated $f(k=1)$! I see no germane difference!
- James Stewart's _Calculus Early Transcendentals_ (2011 7e), p xxvii, Diagnostic Test C: Functions.
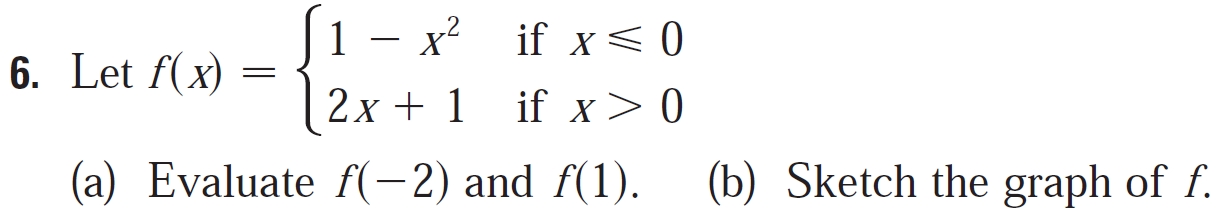
- Ron Larson's _Calculus_ (2018 11e), p 20.
