Post History
#2: Post edited
by
Wolgwang
·
2021-09-02T14:14:13Z (over 2 years ago)
Inserted text and MathJax from the images for better look and search efficiency
How can I visualize the Law of Total Probability with extra conditioning?
- How can I pictorialized this Theorem 2.4.3? As you can see below, I edited a picture by drawing E inside B.. Is my edit correct? Can my edit be improved?
>- Blitzstein, *Introduction to Probability* (2019 2 ed), Chapter 1, p 60.
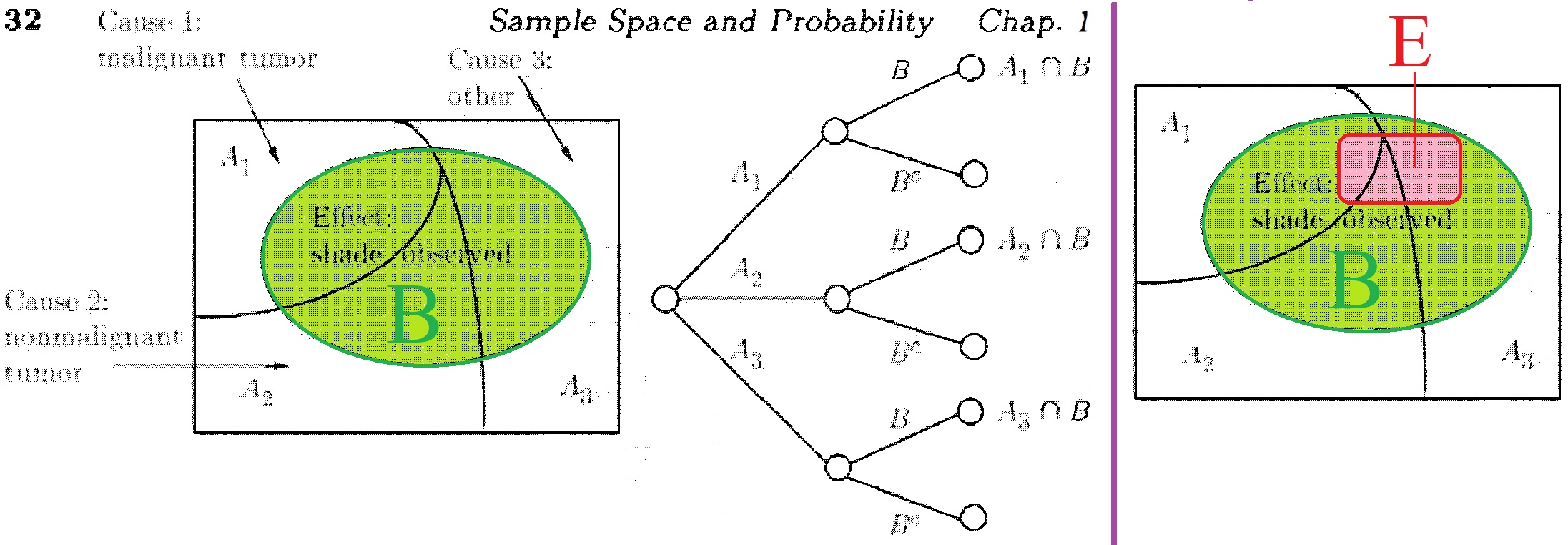- Bertsekas, *Introduction to Probability* (2008 2e), p 32, Fig. 1.14.
- How can I pictorialized this Theorem 2.4.3? As you can see below, I edited a picture by drawing E inside B.. Is my edit correct? Can my edit be improved?
- >**Theorem 2.4.3** (LOTP with extra conditioning). Let $A_{1}, \ldots, A_{n}$ be a partition of
- S. Provided that $P\left(A_{i} \cap E\right)>0$ for all $i$, we have
- $$
- P(B \mid E)=\sum_{i=1}^{n} P\left(B \mid A_{i}, E\right) P\left(A_{i} \mid E\right)
- $$
- Blitzstein, *Introduction to Probability* (2019 2 ed), Chapter 1, p 60.
- 
- Bertsekas, *Introduction to Probability* (2008 2e), p 32, Fig. 1.14.
#1: Initial revision
by
DNB
·
2021-07-28T00:06:49Z (over 2 years ago)
How can I visualize the Law of Total Probability with extra conditioning?
How can I pictorialized this Theorem 2.4.3? As you can see below, I edited a picture by drawing E inside B.. Is my edit correct? Can my edit be improved? > Blitzstein, *Introduction to Probability* (2019 2 ed), Chapter 1, p 60.  Bertsekas, *Introduction to Probability* (2008 2e), p 32, Fig. 1.14.