Post History
#2: Post edited
by
Wolgwang
·
2021-09-02T14:15:09Z (over 3 years ago)
Inserted text and MathJax from the images for better look and search efficiency
Why aren't the "21 possibilities here" NOT equally likely?
Please see the last sentence below, that I underlined in red.- Blitzstein. *Introduction to Probability* (2019 2 ed). Pp. 10-11.
- Please see the last sentence below, that I highlighted in red.
- <hr>
- Example $1.4 .5$ (Ice cream cones). Suppose you are buying an ice cream cone. You can choose whether to have a cake cone or a waffle cone, and whether to have chocolate, vanilla, or strawberry as your flavor. This decision process can be visualized with a tree diagram, as in Figure.
- 
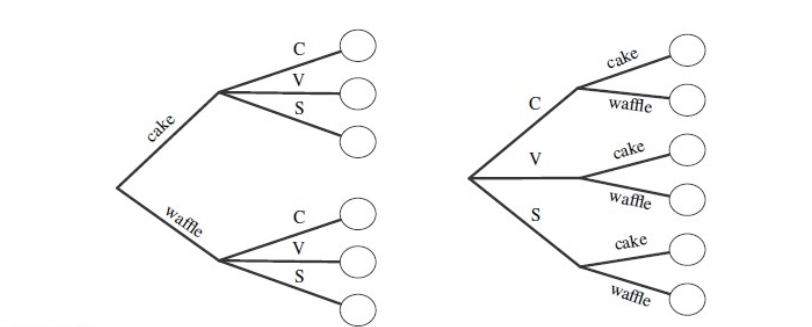
- Tree diagram for choosing an ice cream cone. Regardless of whether the type of cone or the flavor is chosen first, there are $2 \cdot 3=3 \cdot 2=6$ possibilities.
- By the multiplication rule, there are $2 \cdot 3=6$ possibilities. This is a very simple example, but is worth thinking through in detail as a foundation for thinking about and visualizing more complicated examples. Soon we will encounter examples where drawing the tree in a legible size would take up more space than exists in the known universe, yet where conceptually we can still think in terms of the ice cream example. Some things to note:
- 1. It doesn't matter whether you choose the type of cone first ("I'd like a waffle cone with chocolate ice cream") or the flavor first ("I'd like chocolate ice cream on a waffle cone"). Either way, there are $2 \cdot 3=3 \cdot 2=6$ possibilities.
- 2. It doesn't matter whether the same flavors are available on a cake cone as on a waffle cone. What matters is that there are exactly 3 flavor choices for each cone choice. If for some strange reason it were forbidden to have chocolate ice cream on a waffle cone, with no substitute flavor available (aside from vanilla and strawberry), there would be $3+2=5$ possibilities and the multiplication rule wouldn't apply. In larger examples, such complications could make counting the number of possibilities vastly more difficult.
- Now suppose you buy two ice cream cones on a certain day, one in the afternoon and the other in the evening. Write, for example, (cakeC, waffleV) to mean a cake cone with chocolate in the afternoon, followed by a waffle cone with vanilla in the evening. By the multiplication rule, there are $6^{2}=36$ possibilities in your delicious compound experiment.
- But what if you're only interested in what kinds of ice cream cones you had that day, not the order in which you had them, so you don't want to distinguish, for example, between (cakeC, waffleV) and (waffleV, cakeC)? Are there now $36 / 2=18$ possibilities? No, since possibilities like (cakeC, cakeC) were already only listed once each. There are $6 \cdot 5=30$ ordered possibilities $(x, y)$ with $x \neq y$, which turn into 15 possibilities if we treat $(x, y)$ as equivalent to $(y, x)$, plus 6 possibilities of the form $(x, x)$, giving a total of 21 possibilities. Note that if the 36 original ordered pairs $(x, y)$ are equally likely, $\color{red}{\text{then the 21 possibilities here are not equally likely.}}$
- [Original image](https://i.ibb.co/qjWcF0y/Codidact.jpg)
- Blitzstein. *Introduction to Probability* (2019 2 ed). Pp. 10-11.
#1: Initial revision
by
DNB
·
2021-07-09T03:59:27Z (over 3 years ago)
Why aren't the "21 possibilities here" NOT equally likely?
Please see the last sentence below, that I underlined in red.  Blitzstein. *Introduction to Probability* (2019 2 ed). Pp. 10-11.