Post History
#2: Post edited
- 1. Technically, the $\color{red}{10}$ quoted below should be 9.99, because $1% \times 999 = 9.99%$. Anyways, why $\Pr(diseased|+ test) = \dfrac{1 \text{ true positive}}{9.9 \text{ false positives} + \color{limegreen}{1 \text{ true positive}}}$?
- Why isn't $\Pr(diseased|+ test) = \dfrac{1 \text{ true positive}}{9.9 \text{ false positives}}$?
- 2. To help me better understand, can you please fill in this picture from [this Jan 10 2020 article by Prateek Karkare](https://medium.com/x8-the-ai-community/a-simple-introduction-to-naive-bayes-23538a0395a)?
- 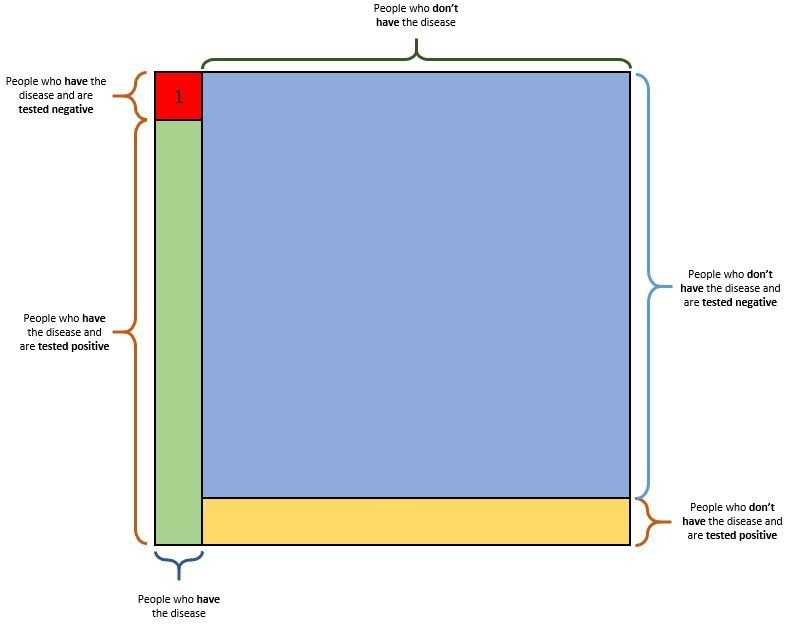
- >I asked the following: “Suppose a rare medical condition is present in 1 of 1,000 adults, but until recently there was no way to check whether you have the condition. However, a recently developed test to check for the condition is 99 percent accurate. You decide to take the test and the result is positive, indicating that the condition is present. What is your judgment of the chance, in percent, that you have the condition?” Almost half of the more than 300 respondents thought the chance they had the disease was 99 percent, approximately a quarter had an answer between 3 percent and 15 percent, and the remaining quarter were spread thinly over the entire range from 0 to 95 percent. The correct answer is “9 percent,” which is almost shocking to many people.
- The logic can be explained in simple terms as follows. Suppose there are 1,000 random adults who are to be tested. On average, we would expect only 1 of these adults to have the disease and the test for that individual would almost surely be positive. This gives us 1 positive test. Also, we would expect 999 adults not to have the disease. With an error rate of 1 percent, we would expect essentially $\color{red}{10}$ of these individuals to have a positive test result. Thus, for the 1,000 individuals, we would expect an average of 11 positive tests, only 1 of which was for an individual with the rare medical condition. Thus, only **1 of 11 [Emphasis mine]**—or 9 percent—of those with the positive test result really have the rare medical condition. Research in the decision sciences has frequently shown that individuals’ intuitions in probabilistic situations are far from accurate.
Paul Slovic, *The Irrational Economist* (2010), pages 245.
- 1. Technically, the $\color{red}{10}$ quoted below should be 9.99, because $1% \times 999 = 9.99%$. Anyways, why $\Pr(diseased|+ test) = \dfrac{1 \text{ true positive}}{9.9 \text{ false positives} + \color{limegreen}{1 \text{ true positive}}}$?
- Why isn't $\Pr(diseased|+ test) = \dfrac{1 \text{ true positive}}{9.9 \text{ false positives}}$?
- 2. To help me better understand, can you please fill in this picture from [this Jan 10 2020 article by Prateek Karkare](https://medium.com/x8-the-ai-community/a-simple-introduction-to-naive-bayes-23538a0395a)?
- 
- >I asked the following: “Suppose a rare medical condition is present in 1 of 1,000 adults, but until recently there was no way to check whether you have the condition. However, a recently developed test to check for the condition is 99 percent accurate. You decide to take the test and the result is positive, indicating that the condition is present. What is your judgment of the chance, in percent, that you have the condition?” Almost half of the more than 300 respondents thought the chance they had the disease was 99 percent, approximately a quarter had an answer between 3 percent and 15 percent, and the remaining quarter were spread thinly over the entire range from 0 to 95 percent. The correct answer is “9 percent,” which is almost shocking to many people.
- The logic can be explained in simple terms as follows. Suppose there are 1,000 random adults who are to be tested. On average, we would expect only 1 of these adults to have the disease and the test for that individual would almost surely be positive. This gives us 1 positive test. Also, we would expect 999 adults not to have the disease. With an error rate of 1 percent, we would expect essentially $\color{red}{10}$ of these individuals to have a positive test result. Thus, for the 1,000 individuals, we would expect an average of 11 positive tests, only 1 of which was for an individual with the rare medical condition. Thus, only **1 of 11 [Emphasis mine]**—or 9 percent—of those with the positive test result really have the rare medical condition. Research in the decision sciences has frequently shown that individuals’ intuitions in probabilistic situations are far from accurate.
- Paul Slovic, *The Irrational Economist* (2010), page 245.
#1: Initial revision
Why isn't $\Pr(diseased|+ test) = \dfrac{\text{number of true positives}}{\text{number of false positives}}$?
1. Technically, the $\color{red}{10}$ quoted below should be 9.99, because $1% \times 999 = 9.99%$. Anyways, why $\Pr(diseased|+ test) = \dfrac{1 \text{ true positive}}{9.9 \text{ false positives} + \color{limegreen}{1 \text{ true positive}}}$?
Why isn't $\Pr(diseased|+ test) = \dfrac{1 \text{ true positive}}{9.9 \text{ false positives}}$?
2. To help me better understand, can you please fill in this picture from [this Jan 10 2020 article by Prateek Karkare](https://medium.com/x8-the-ai-community/a-simple-introduction-to-naive-bayes-23538a0395a)?

>I asked the following: “Suppose a rare medical condition is present in 1 of 1,000 adults, but until recently there was no way to check whether you have the condition. However, a recently developed test to check for the condition is 99 percent accurate. You decide to take the test and the result is positive, indicating that the condition is present. What is your judgment of the chance, in percent, that you have the condition?” Almost half of the more than 300 respondents thought the chance they had the disease was 99 percent, approximately a quarter had an answer between 3 percent and 15 percent, and the remaining quarter were spread thinly over the entire range from 0 to 95 percent. The correct answer is “9 percent,” which is almost shocking to many people.
The logic can be explained in simple terms as follows. Suppose there are 1,000 random adults who are to be tested. On average, we would expect only 1 of these adults to have the disease and the test for that individual would almost surely be positive. This gives us 1 positive test. Also, we would expect 999 adults not to have the disease. With an error rate of 1 percent, we would expect essentially $\color{red}{10}$ of these individuals to have a positive test result. Thus, for the 1,000 individuals, we would expect an average of 11 positive tests, only 1 of which was for an individual with the rare medical condition. Thus, only **1 of 11 [Emphasis mine]**—or 9 percent—of those with the positive test result really have the rare medical condition. Research in the decision sciences has frequently shown that individuals’ intuitions in probabilistic situations are far from accurate.
Paul Slovic, *The Irrational Economist* (2010), pages 245.


















