Post History
#4: Post edited
by
Chgg Clou
·
2021-06-07T07:49:58Z (over 3 years ago)
Please see the bolden phrase below. Did the authors mix up which is certain, and which isn't?- 1. Isn't the outcome of airplane crashes AMBIGUOUS? Because they aren't fatal?
- But the author wrote "almost always certain". And in Table 12.1, the author regarded this probability "precise".
- 2. Isn't the probability of airplane crashes PRECISE? Because the probability of crashes has been teensy — even back when this book was published in 2010?
- But in Table 12.1, the author regarded this probability "ambiguous".
- > Most of the research on ambiguity focuses on vague probabilities. However, in some situations, uncertainty can also exist with respect to outcomes (i.e., whether the outcome is precisely known or not). Table 12.1 presents some stylized examples of this taxonomy of precise/imprecise probabilities and outcomes. For instance, on a roulette table, the chances of winning or losing and the amount at stake are well specified; hence this example falls into the category of precise probabilities/precise outcomes. **The outcome of an airplane crash is almost always certain, whereas the probability of having such an accident is not—a case of ambiguous probabilities/precise outcomes. [Emphasis mine]** We could estimate (more or less) our chances of getting a tax audit depending on our income bracket, but it is difficult to foresee any possible penalties—a case of precise probabilities/ambiguous outcomes. And, finally, if we do not have a clear prediction about the probability and the magnitude of damage from an earthquake, we are looking at a case of ambiguous probabilities/ambiguous outcomes.
- >
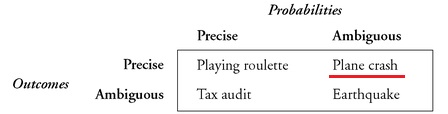
- >TABLE 12.1 Examples for Different Sources of Ambiguity
- Paul Slovic, *The Irrational Economist* (2010), page 111.
- Please see the bolden phrase and Table 12.1 below. For plane crashes, did the author mix up which (probability or outcome) is ambiguous, and which is precise?
- 1. Isn't the outcome of airplane crashes AMBIGUOUS? Because they aren't fatal?
- But the author wrote "almost always certain". And in Table 12.1, the author regarded this probability "precise".
- 2. Isn't the probability of airplane crashes PRECISE? Because the probability of crashes has been teensy — even back when this book was published in 2010?
- But in Table 12.1, the author regarded this probability "ambiguous".
- > Most of the research on ambiguity focuses on vague probabilities. However, in some situations, uncertainty can also exist with respect to outcomes (i.e., whether the outcome is precisely known or not). Table 12.1 presents some stylized examples of this taxonomy of precise/imprecise probabilities and outcomes. For instance, on a roulette table, the chances of winning or losing and the amount at stake are well specified; hence this example falls into the category of precise probabilities/precise outcomes. **The outcome of an airplane crash is almost always certain, whereas the probability of having such an accident is not—a case of ambiguous probabilities/precise outcomes. [Emphasis mine]** We could estimate (more or less) our chances of getting a tax audit depending on our income bracket, but it is difficult to foresee any possible penalties—a case of precise probabilities/ambiguous outcomes. And, finally, if we do not have a clear prediction about the probability and the magnitude of damage from an earthquake, we are looking at a case of ambiguous probabilities/ambiguous outcomes.
- >
- >TABLE 12.1 Examples for Different Sources of Ambiguity
- Paul Slovic, *The Irrational Economist* (2010), page 111.
#3: Post edited
by
Chgg Clou
·
2021-06-07T07:49:12Z (over 3 years ago)
Please see the bolden phrase below. Did the authors mix up the two? Isn't the outcome of airplane crashes AMBIGUOUS — they aren't fatal? Isn't the probability of airplane crashes PRECISE — because they've been teensy — even back when this book was published in 2010?- > Most of the research on ambiguity focuses on vague probabilities. However, in some situations, uncertainty can also exist with respect to outcomes (i.e., whether the outcome is precisely known or not). Table 12.1 presents some stylized examples of this taxonomy of precise/imprecise probabilities and outcomes. For instance, on a roulette table, the chances of winning or losing and the amount at stake are well specified; hence this example falls into the category of precise probabilities/precise outcomes. **The outcome of an airplane crash is almost always certain, whereas the probability of having such an accident is not—a case of ambiguous probabilities/precise outcomes. [Emphasis mine]** We could estimate (more or less) our chances of getting a tax audit depending on our income bracket, but it is difficult to foresee any possible penalties—a case of precise probabilities/ambiguous outcomes. And, finally, if we do not have a clear prediction about the probability and the magnitude of damage from an earthquake, we are looking at a case of ambiguous probabilities/ambiguous outcomes.
- >
- >TABLE 12.1 Examples for Different Sources of Ambiguity
- Paul Slovic, *The Irrational Economist* (2010), page 111.
- Please see the bolden phrase below. Did the authors mix up which is certain, and which isn't?
- 1. Isn't the outcome of airplane crashes AMBIGUOUS? Because they aren't fatal?
- But the author wrote "almost always certain". And in Table 12.1, the author regarded this probability "precise".
- 2. Isn't the probability of airplane crashes PRECISE? Because the probability of crashes has been teensy — even back when this book was published in 2010?
- But in Table 12.1, the author regarded this probability "ambiguous".
- > Most of the research on ambiguity focuses on vague probabilities. However, in some situations, uncertainty can also exist with respect to outcomes (i.e., whether the outcome is precisely known or not). Table 12.1 presents some stylized examples of this taxonomy of precise/imprecise probabilities and outcomes. For instance, on a roulette table, the chances of winning or losing and the amount at stake are well specified; hence this example falls into the category of precise probabilities/precise outcomes. **The outcome of an airplane crash is almost always certain, whereas the probability of having such an accident is not—a case of ambiguous probabilities/precise outcomes. [Emphasis mine]** We could estimate (more or less) our chances of getting a tax audit depending on our income bracket, but it is difficult to foresee any possible penalties—a case of precise probabilities/ambiguous outcomes. And, finally, if we do not have a clear prediction about the probability and the magnitude of damage from an earthquake, we are looking at a case of ambiguous probabilities/ambiguous outcomes.
- >
- >TABLE 12.1 Examples for Different Sources of Ambiguity
- Paul Slovic, *The Irrational Economist* (2010), page 111.
#2: Question closed
by
Monica Cellio
·
2021-06-06T23:53:36Z (over 3 years ago)
#1: Initial revision
by
Chgg Clou
·
2021-06-06T08:26:15Z (over 3 years ago)
How's the outcome of airplane crashes almost always certain, but the probability is not?
Please see the bolden phrase below. Did the authors mix up the two? Isn't the outcome of airplane crashes AMBIGUOUS — they aren't fatal? Isn't the probability of airplane crashes PRECISE — because they've been teensy — even back when this book was published in 2010? > Most of the research on ambiguity focuses on vague probabilities. However, in some situations, uncertainty can also exist with respect to outcomes (i.e., whether the outcome is precisely known or not). Table 12.1 presents some stylized examples of this taxonomy of precise/imprecise probabilities and outcomes. For instance, on a roulette table, the chances of winning or losing and the amount at stake are well specified; hence this example falls into the category of precise probabilities/precise outcomes. **The outcome of an airplane crash is almost always certain, whereas the probability of having such an accident is not—a case of ambiguous probabilities/precise outcomes. [Emphasis mine]** We could estimate (more or less) our chances of getting a tax audit depending on our income bracket, but it is difficult to foresee any possible penalties—a case of precise probabilities/ambiguous outcomes. And, finally, if we do not have a clear prediction about the probability and the magnitude of damage from an earthquake, we are looking at a case of ambiguous probabilities/ambiguous outcomes. > >TABLE 12.1 Examples for Different Sources of Ambiguity Paul Slovic, *The Irrational Economist* (2010), page 111.