Post History
#4: Post edited
by
Peter Taylor
·
2021-05-14T14:07:28Z (over 3 years ago)
Complete argument
This image matches the description in the question (note that, in violation of what I consider to be conventional, $O$ is not the centre of the circle but the midpoint of $AD$). $OG$ is perpendicular to $OD$.Show that $AOG$, $DOG$, $DFG$ and $CDF$ are all congruent. Then since the area of a triangle is a half of the base times the height, $$\tfrac{1}{2} \overline{AF} \cdot \overline{DF} = 3 \cdot \tfrac{1}{2} \overline{CF} \cdot \overline{DF}$$Most of that follows from these basics:* angles at a line sum to 180* angles in a triangle sum to 180* two sides and their enclosing angle completely determine a triangleThat just leaves finding a suitably basic argument that $FD$ is perpendicular to $AC$.
- This image matches the description in the question (note that, in violation of what I consider to be conventional, $O$ is not the centre of the circle but the midpoint of $AD$). I add a perpendicular to $AD$ from $O$ which intersects $AC$ at $G$, and lines $OF$ and $DG$ which intersect at $H$.
- 
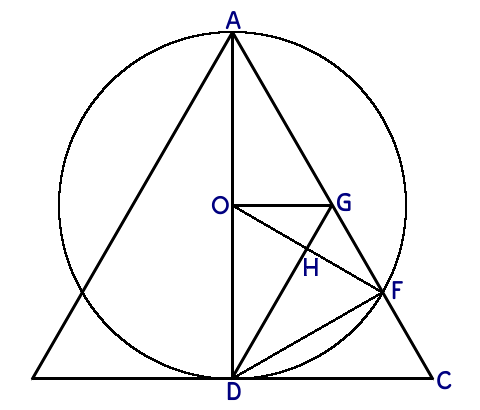
- The key idea is to show that $AOG$, $DOG$, $DFG$ and $CDF$ are all congruent. Then since the area of a triangle is a half of the base times the height, $$\tfrac{1}{2} \overline{AF} \cdot \overline{DF} = 3 \cdot \tfrac{1}{2} \overline{CF} \cdot \overline{DF}$$
- One argument which uses fairly basic lemmata and certainly makes no mention of similar triangles is as follows:
- 1. Angle $ACD = 60^\circ$ because it's an angle of an equilateral triangle.
- 2. Angle $CAD = 30^\circ$ because AD is a bisector.
- 3. $\overline{AO} = \overline{OD}$ by definition of $O$.
- 4. Angles $AOG = DOG = 90^\circ$ by definition of $G$.
- 5. Angle $AGO = 60^\circ$ by sum of angles in a triangle.
- 6. $AOG$ is congruent to $DOG$ by side-angle-side.
- 7. Angle $ODG = 30^\circ$ and $OGD = 60^\circ$ in consequence.
- 8. Angle $DGF = 60^\circ$ by sum of angles on a line.
- 9. $AO$ and $OF$ are radii of the circle, so $AOF$ is isosceles and angle $OFA = OAF = 30^\circ$.
- 10. Angle $FOG = 30^\circ$ by sum of angles in a triangle.
- 11. Angle $DOF = 60^\circ$ by e.g. sum of angles on a line.
- 12. $OD$ and $OF$ are radii of the circle, so $DOF$ is isosceles and angle $ODF = OFD$. But since angles in a triangle sum to $180^\circ$ and $DOF = 60^\circ$ that means that $ODF = OFD = 60^\circ$.
- 13. The angles of $OGD$ and $DFG$ are all known and they share edge $DG$, so we have enough to show that they're congruent.
- 14. Angle $DFC = 90^\circ$ by sum of angles on a line.
- 15. Angle $FDC = 30^\circ$ by e.g. sum of angles in a triangle.
- 16. The angles of $DFG$ and $DFC$ are known and they share edge $DF$, so we have enough to show that they're congruent.
#3: Post edited
by
Peter Taylor
·
2021-05-14T12:51:54Z (over 3 years ago)
Actually I was a bit too blithe in how easy it is to show congruence
- This image matches the description in the question (note that, in violation of what I consider to be conventional, $O$ is not the centre of the circle but the midpoint of $AD$). $OG$ is perpendicular to $OD$.
- 
By using the facts that angles at a line sum to 180 and angles in a triangle sum to 180 you can show that $AOG$, $DOG$, $DFG$ and $CDF$ are all congruent. Then since the area of a triangle is a half of the base times the height, $$\tfrac{1}{2} \overline{AF} \cdot \overline{DF} = 3 \cdot \tfrac{1}{2} \overline{CF} \cdot \overline{DF}$$
- This image matches the description in the question (note that, in violation of what I consider to be conventional, $O$ is not the centre of the circle but the midpoint of $AD$). $OG$ is perpendicular to $OD$.
- 
- Show that $AOG$, $DOG$, $DFG$ and $CDF$ are all congruent. Then since the area of a triangle is a half of the base times the height, $$\tfrac{1}{2} \overline{AF} \cdot \overline{DF} = 3 \cdot \tfrac{1}{2} \overline{CF} \cdot \overline{DF}$$
- Most of that follows from these basics:
- * angles at a line sum to 180
- * angles in a triangle sum to 180
- * two sides and their enclosing angle completely determine a triangle
- That just leaves finding a suitably basic argument that $FD$ is perpendicular to $AC$.
#2: Post edited
by
Peter Taylor
·
2021-05-14T12:35:50Z (over 3 years ago)
This image matches the description in the question (note that, in violation of what I consider to be conventional, $O$ is not the centre of the circle but the bisector of $AD$). $OG$ is perpendicular to $OD$.- 
- By using the facts that angles at a line sum to 180 and angles in a triangle sum to 180 you can show that $AOG$, $DOG$, $DFG$ and $CDF$ are all congruent. Then since the area of a triangle is a half of the base times the height, $$\tfrac{1}{2} \overline{AF} \cdot \overline{DF} = 3 \cdot \tfrac{1}{2} \overline{CF} \cdot \overline{DF}$$
- This image matches the description in the question (note that, in violation of what I consider to be conventional, $O$ is not the centre of the circle but the midpoint of $AD$). $OG$ is perpendicular to $OD$.
- 
- By using the facts that angles at a line sum to 180 and angles in a triangle sum to 180 you can show that $AOG$, $DOG$, $DFG$ and $CDF$ are all congruent. Then since the area of a triangle is a half of the base times the height, $$\tfrac{1}{2} \overline{AF} \cdot \overline{DF} = 3 \cdot \tfrac{1}{2} \overline{CF} \cdot \overline{DF}$$
#1: Initial revision
by
Peter Taylor
·
2021-05-14T12:35:29Z (over 3 years ago)
This image matches the description in the question (note that, in violation of what I consider to be conventional, $O$ is not the centre of the circle but the bisector of $AD$). $OG$ is perpendicular to $OD$.
By using the facts that angles at a line sum to 180 and angles in a triangle sum to 180 you can show that $AOG$, $DOG$, $DFG$ and $CDF$ are all congruent. Then since the area of a triangle is a half of the base times the height, $$\tfrac{1}{2} \overline{AF} \cdot \overline{DF} = 3 \cdot \tfrac{1}{2} \overline{CF} \cdot \overline{DF}$$