Post History

37%

+1 −3

Q&A How can I generalize a picture for the Mean Value Theorem to the Generalized MVT?

1 answer · posted 3y ago by TextKit‭ · edited 3y ago by TextKit‭

Question calculus visualization

#3: Post edited by $user avatar$ TextKit‭ · 2021-02-11T22:16:44Z (about 3 years ago)

Copy Link

Raw

Markdown

How can I transmogrify this figure for the [Generalized MVT](https://math.stackexchange.com/q/296176)? If $f$ and $g$ are continuous
on the closed interval $[a, b]$ and differentiable on the open interval $(a, b)$,
then $\exists$ $c ∈ (a, b)$ $
\cfrac{f'(c)}{g'(c)} = \cfrac{f(b)-f(a)}{g(b)-g(a)}$.
~~Please don't just change the t-axis to $g(t)$.~~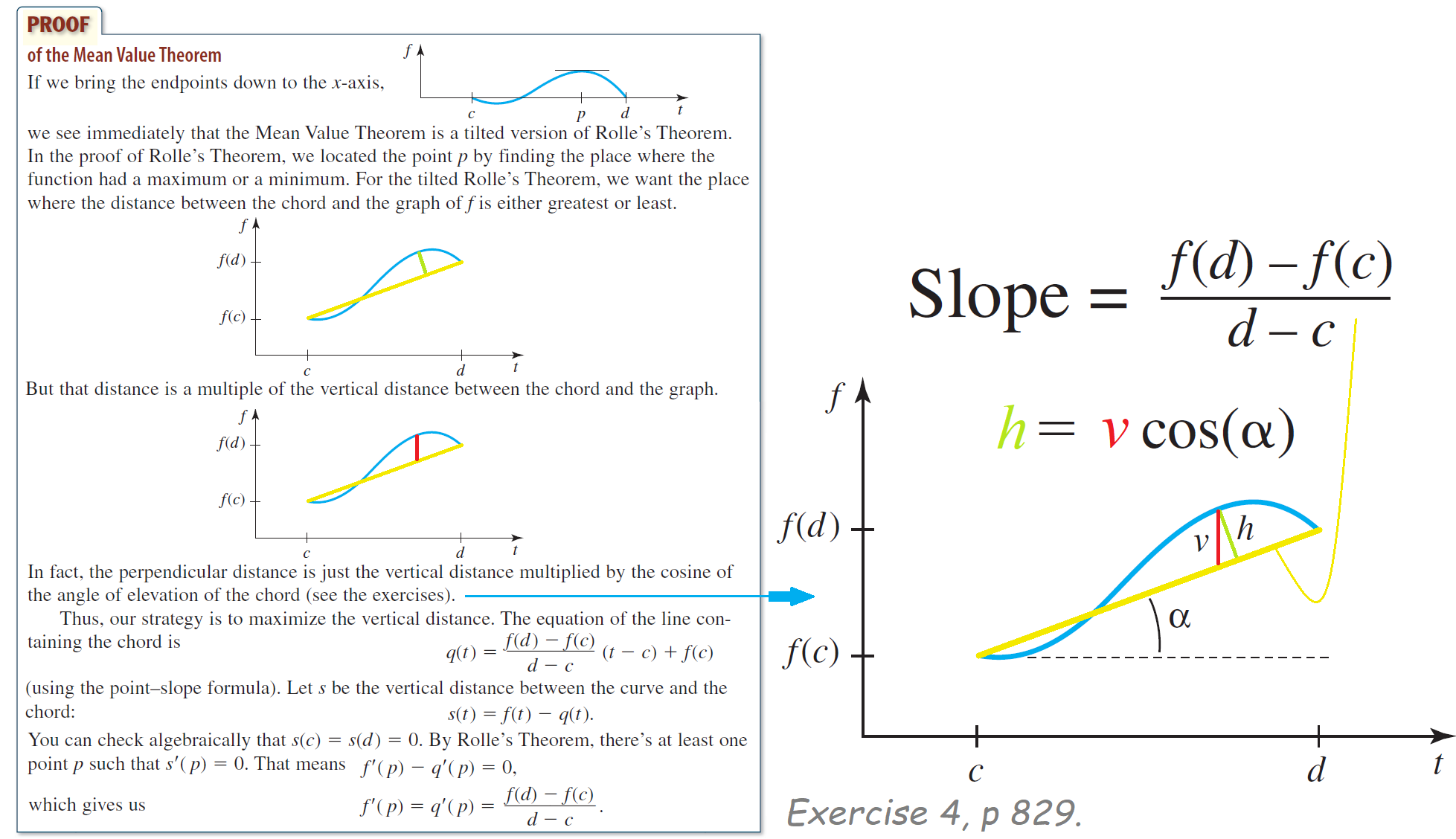
![Image alt text](https://math.codidact.com/uploads/anR9gNuPbWn3cFdpVignwDZK)
[*Calculus: The Language Of Change*](https://www.amazon.com/Calculus-Language-David-W-Cohen/dp/0763729477) (2005)
by David W. Cohen, James M. Henle. [pp. 827-829](https://books.google.com/books?id=QNfZls4urMoC&pg=PA827&lpg=PA827&dq=mean+value+theorem+proof+tilt&source=bl&ots=WjLggTfZBQ&sig=5hcMBO1xjIv5xt7Fejr9C7LQkoM&hl=fr&sa=X&ei=vz0PU8KbOundigeLv4DwDQ&redir_esc=y#v=onepage&q&f=true). The original colored in just blue. I annotated and added more colors.

How can I transmogrify this figure for the [Generalized MVT](https://math.stackexchange.com/q/296176)? If $f$ and $g$ are continuous
on the closed interval $[a, b]$ and differentiable on the open interval $(a, b)$,
then $\exists$ $c ∈ (a, b) \ni
\cfrac{f'(c)}{g'(c)} = \cfrac{f(b)-f(a)}{g(b)-g(a)}$.
Please answer with a picture. Please edit my scan, and draw or write in what you mean. Don't just change the t-axis to $g(t)$.
![Image alt text](https://math.codidact.com/uploads/anR9gNuPbWn3cFdpVignwDZK)
[*Calculus: The Language Of Change*](https://www.amazon.com/Calculus-Language-David-W-Cohen/dp/0763729477) (2005)
by David W. Cohen, James M. Henle. [pp. 827-829](https://books.google.com/books?id=QNfZls4urMoC&pg=PA827&lpg=PA827&dq=mean+value+theorem+proof+tilt&source=bl&ots=WjLggTfZBQ&sig=5hcMBO1xjIv5xt7Fejr9C7LQkoM&hl=fr&sa=X&ei=vz0PU8KbOundigeLv4DwDQ&redir_esc=y#v=onepage&q&f=true). The original colored in just blue. I annotated and added more colors.

calculus visualization

#2: Post edited by $user avatar$ TextKit‭ · 2021-02-04T02:42:24Z (over 3 years ago)

Copy Link

Raw

Markdown

How can I transmogrify this figure for the [Generalized MVT](https://math.stackexchange.com/q/296176)? If $f$ and $g$ are continuous
on the closed interval $[a, b]$ and differentiable on the open interval $(a, b)$,
then $\exists$ $c ∈ (a, b)$ $
\cfrac{f'(c)}{g'(c)} = \cfrac{f(b)-f(a)}{g(b)-g(a)}$.
Please don't just change the t-axis to $g(t)$.
~~![Image alt text](https://math.codidact.com/uploads/KHsHGXQoG5sq4ZNY6t419B4o)~~
[*Calculus: The Language Of Change*](https://www.amazon.com/Calculus-Language-David-W-Cohen/dp/0763729477) (2005)
by David W. Cohen, James M. Henle. [pp. 827-829](https://books.google.com/books?id=QNfZls4urMoC&pg=PA827&lpg=PA827&dq=mean+value+theorem+proof+tilt&source=bl&ots=WjLggTfZBQ&sig=5hcMBO1xjIv5xt7Fejr9C7LQkoM&hl=fr&sa=X&ei=vz0PU8KbOundigeLv4DwDQ&redir_esc=y#v=onepage&q&f=true). The original colored in just blue. I annotated and added more colors.

How can I transmogrify this figure for the [Generalized MVT](https://math.stackexchange.com/q/296176)? If $f$ and $g$ are continuous
on the closed interval $[a, b]$ and differentiable on the open interval $(a, b)$,
then $\exists$ $c ∈ (a, b)$ $
\cfrac{f'(c)}{g'(c)} = \cfrac{f(b)-f(a)}{g(b)-g(a)}$.
Please don't just change the t-axis to $g(t)$.
![Image alt text](https://math.codidact.com/uploads/anR9gNuPbWn3cFdpVignwDZK)
[*Calculus: The Language Of Change*](https://www.amazon.com/Calculus-Language-David-W-Cohen/dp/0763729477) (2005)
by David W. Cohen, James M. Henle. [pp. 827-829](https://books.google.com/books?id=QNfZls4urMoC&pg=PA827&lpg=PA827&dq=mean+value+theorem+proof+tilt&source=bl&ots=WjLggTfZBQ&sig=5hcMBO1xjIv5xt7Fejr9C7LQkoM&hl=fr&sa=X&ei=vz0PU8KbOundigeLv4DwDQ&redir_esc=y#v=onepage&q&f=true). The original colored in just blue. I annotated and added more colors.

calculus visualization

#1: Initial revision by $user avatar$ TextKit‭ · 2021-02-04T02:22:15Z (over 3 years ago)

Copy Link

Raw

Markdown

How can I generalize a picture for the Mean Value Theorem to the Generalized MVT?

How can I transmogrify this figure for the [Generalized MVT](https://math.stackexchange.com/q/296176)? If $f$ and $g$ are continuous
on the closed interval $[a, b]$ and differentiable on the open interval $(a, b)$,
then $\exists$  $c ∈ (a, b)$ $
\cfrac{f'(c)}{g'(c)} = \cfrac{f(b)-f(a)}{g(b)-g(a)}$.
 

Please don't just change the t-axis to $g(t)$.

![Image alt text](https://math.codidact.com/uploads/KHsHGXQoG5sq4ZNY6t419B4o)

[*Calculus: The Language Of Change*](https://www.amazon.com/Calculus-Language-David-W-Cohen/dp/0763729477) (2005)
by David W. Cohen, James M. Henle. [pp. 827-829](https://books.google.com/books?id=QNfZls4urMoC&pg=PA827&lpg=PA827&dq=mean+value+theorem+proof+tilt&source=bl&ots=WjLggTfZBQ&sig=5hcMBO1xjIv5xt7Fejr9C7LQkoM&hl=fr&sa=X&ei=vz0PU8KbOundigeLv4DwDQ&redir_esc=y#v=onepage&q&f=true). The original colored in just blue. I annotated and added more colors.

calculus visualization

Communities

Post History