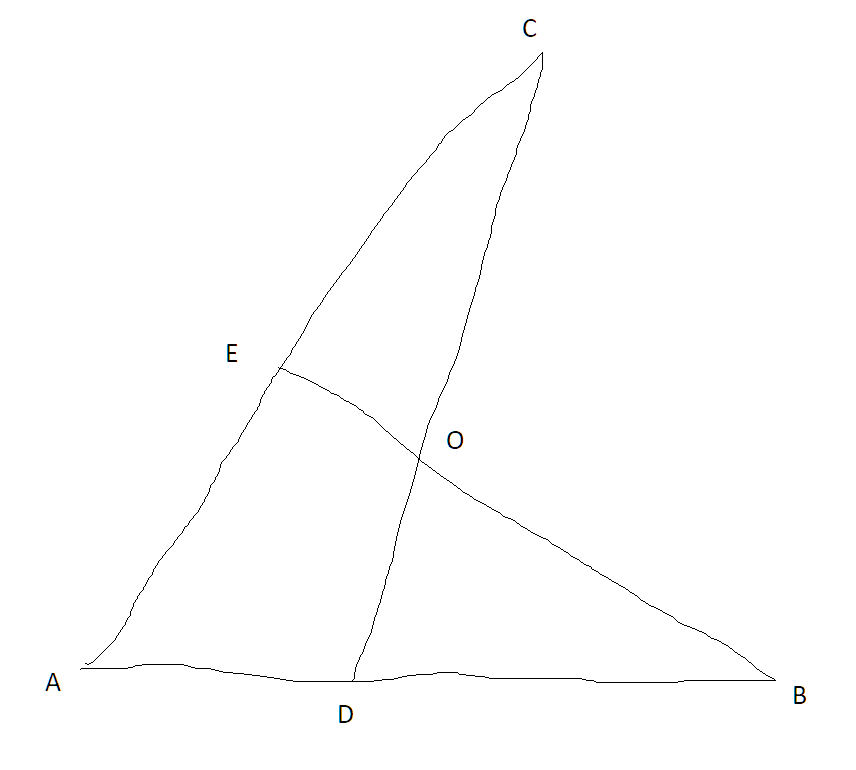
My kid was assigned this problem:
> Given
>
> 
>
> $\overline{AC}\cong\overline{AB}$ and $\angle B\cong\angle C$.
>
> Prove (a) $\overline{CE}\cong\overline{BD}$ and (b) $\overline{OB}\cong\overline{OC}$.
(I apologize for the ugly sketch. All lines that seem like they're meant to be straight are.)
The most direct way seems to be: Prove triangles $CAD$ and $BAE$ congruent (easy). Prove triangles $COE$ and $BOD$ similar (easy). Prove triangles $COE$ and $BOD$ congruent because they're similar and have the same area (by subtracting the common area of $ADOE$). The rest follows immediately.
The problem is — I don't recall ever seeing in a high-school geometry text the proposition "If two triangles are similar and have the same area, they're congruent". Or at least not as a method of proof for proving triangles congruent. So I guess my question is: Why not? It would certainly come in handy for cases like this. (Or am I wrong that it's correct in general?)
As a secondary question, is there a better way to do the problem above?
msh210
·
2020-10-02T09:50:57Z (over 3 years ago)